虛（數）與實（數）

以下是兩個常見的數學謎語：

1.　背着喇叭；
2.　大夫診症；

謎底稍後揭曉。

在中學時期，我們知道 ax² +bx+c=0 的兩個解可表達成 (-b ± √ (b² -4ac))/2。

原來 ax³ +bx² +cx+d=0 的三個解也有一般表達式，最簡單的一個是


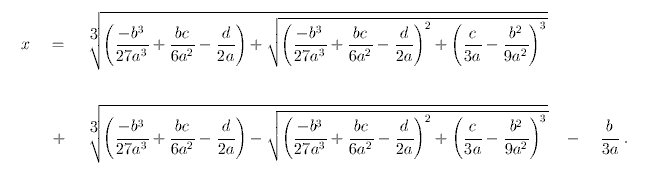
這個解在十六世紀時經已被發現，但卻出現了個問題：考慮 x³ -15x-4=0，它的所有答案是 -3.73, -0.26, 4。若用以上的算式，卻出現不知所謂的 √-109（用計算機試試，九成會送你一個 Error），這條算式似乎用不着！

數學家的解決方法很簡單，首先讓 √-109 = i √109 （這裡i=√-1），然後把i當作一般數字來計，最後所有i會相互抵消！但如 i √109 般的數，令人感覺虛無飄眇，故稱作『虛數』。

這時，人們倒過來說一般的數字是『實數』，即是實在的數。

但正如自然數並不比其他數自然¹，實數的『實』和虛數的『虛』相差其實不大。若考慮二維平面，實數與虛數只是橫軸與縱軸之分而已！

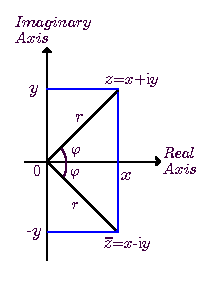這平面稱作複平面，上面的每一點(x,y)代表着x+iy，喚作複數。由此，二維的數出現了，標誌着數字家族新的一頁。在複平面上，『任何複數都有平方根』（e.g. √-4 = 2i，√(2i)=1+i，√(3-4i)=2-i）²，並有着很多不可能在實數出現的特性。

謎語答案：1.　負號；2.　開方。

正數加上負號再開方，便是虛數！

註１：請參看《自然的數？》。
註２：開方只取“正值”，如√4＝2但4的平方根是 ±2，這兒 -4 的平方根是 ±2i，2i 的平方根是 ±(1+i)，3-4i 的平方根是 ±(2-i)。