現代經濟學的第一假設:在可能的情况下,人會尋求利益極大化。
中文副教授唐方方在《信報》及《財華網》刊出題為『義烏商人決策達致「利潤最優化」』中,提出很多人都沒有嘗試賺到盡,好像與這個假設不符。
是真的不符嗎?
世事的難測,即使消耗心力,機關算盡,自以為勝卷在握,不給對手任何餘地;那知人算不如天算,亦因為逼人太甚,沒有妥協空間,可能一切得不嘗失!俗語所云:「機關算盡太聰明」、「凡事留一線,日後好相見」、「錢不可以賺到盡」,所是這個意思。
食蟻獸不會把所有的蟻吃掉,因為它要保證永遠有蟻食;同樣道理,不要嘗試在這刻把錢賺盡,可能就會永遠有錢賺--換句說話,短期不賺最多的錢,長遠可能賺得更多。
明白這個,即使個人真是自私,真的希望尋求利益極大化,亦會留一點睘轉的餘地。結果,就是好像沒有嘗試賺到盡。
不明白這個,但不懂得如何去計算利益極大化,唯有用最簡單的方法,如文中的義烏商人。結果,亦是沒有嘗試賺到盡。
兩種情況,可能當事人都己經賺到盡,不過我們永遠沒法肯定。
最要命的,是不明白這個,亦不明白自已根本不知道如何去計算利益極大化,嘗試去賺到盡。自私加上無知,就是一切災禍(例如污染、濫捕、沙漠化)的根源。
所謂利益極大化,只是經濟學中的一個假設,用來解釋社會行為。祗有很少的一撮人,真的會身體力行,用極複雜的理論,尋找最大的利潤;而當中亦只有更少的一撮人,可以真的達到心目中的最大利潤。
Friday, December 15, 2006
Tuesday, November 21, 2006
世上沒有免費午餐
『世上沒有免費午餐』,由剛過世的經濟學大師佛利民發揚光大,成為家傳戶曉的一句名言。問題是:誰付鈔?
我的朋友說,甘地及德蘭修女無私奉獻,沒有犧牲其他人的利益,是絕對的偉大。不是的,例如他倆都致力幫助所謂賤民階級,其實損害了種姓制度支持者的利益--不過在我們的道德觀念裡,那些人不該擁有這樣的利益。
為甚麼我們的道德觀會比那些種姓制度支持者正確?任由那一位思想家,都說不清楚。不同的道德觀,似乎亦在演化,在競爭在淘汰。
慢 慢地,科學好像成了各種信仰的最大公因數。因為科學可以用實驗來測試,有一個較為客觀的標準。但,這個標準是甚麼,卻沒多少人清楚;結果,不論是商業販 子,或一些宗教頭目,都不約而同的引入了僞科學。市面的不良醫藥廣告固然可惡,但影音使團的地球深度行,真的找到挪亞方舟嗎?
科學與信仰的最大分別,再於前者不容許矛盾存在,而後者卻永遠都充滿矛盾。例如,我相信我們應對所有信念有所包容,但要我包容那些『不包容』的思想,郤有些難度。
有些自以為開通的人,把堅守「傳統道德」的人謔稱為『道德佬』。其實,他們卻不自知地成為另一類道德佬。不同的道德觀都有不同程度的排他性,每個人在其底線上,都是一個道德佬!當你要維護自己的道德時,就要犧牲其他思想的利益,因為『世上沒有免費午餐』。
我的朋友說,甘地及德蘭修女無私奉獻,沒有犧牲其他人的利益,是絕對的偉大。不是的,例如他倆都致力幫助所謂賤民階級,其實損害了種姓制度支持者的利益--不過在我們的道德觀念裡,那些人不該擁有這樣的利益。
為甚麼我們的道德觀會比那些種姓制度支持者正確?任由那一位思想家,都說不清楚。不同的道德觀,似乎亦在演化,在競爭在淘汰。
慢 慢地,科學好像成了各種信仰的最大公因數。因為科學可以用實驗來測試,有一個較為客觀的標準。但,這個標準是甚麼,卻沒多少人清楚;結果,不論是商業販 子,或一些宗教頭目,都不約而同的引入了僞科學。市面的不良醫藥廣告固然可惡,但影音使團的地球深度行,真的找到挪亞方舟嗎?
科學與信仰的最大分別,再於前者不容許矛盾存在,而後者卻永遠都充滿矛盾。例如,我相信我們應對所有信念有所包容,但要我包容那些『不包容』的思想,郤有些難度。
有些自以為開通的人,把堅守「傳統道德」的人謔稱為『道德佬』。其實,他們卻不自知地成為另一類道德佬。不同的道德觀都有不同程度的排他性,每個人在其底線上,都是一個道德佬!當你要維護自己的道德時,就要犧牲其他思想的利益,因為『世上沒有免費午餐』。
Sunday, October 29, 2006
天(道),自然,市場
我們時常談及天(此處等於道) 、自然、市場。這三個概念,看似不同,但細心玩味,似乎是同一個概念的不同面貎。
當我們談及這三個槪念時,似乎經常出現邏輯矛盾:人是道的一部分,人的行為就是天的一部分,怎可以逆天而行?人是自然的一部分,人的行為就是自然的一部分,怎會是違反自然?人是市場的一部分,人的行為就是市場的一部分,怎可能叫作干預市場?
其實看深一層,是有點『成王敗寇』的味道。成功的,就是順應天命、符合自然、服從經濟規律;失敗的,就是逆天而行、破壞自然、搞亂市場運作。
究意有無客觀標準?只可以說,自古以來,人類都相信冥冥中萬物是跟從一定的模式運作。於是,我們憑着『成王敗寇』為例子,然後觀察、研究、學習,嘗試找出這個模式。
當我們掌握了一個模式,會利用它來為自己尋求更大的利益。不過,我們的模式可能是錯,或可能是對但出現不能控制的因素,但我們只能盡力而為--這個便是諺語「謀事在人,成事在天」,或更一般的,就是進化論中的「物競天擇」。
有人指出,為自己尋求最大的利益,是自私的行徑。但其實,聖雄甘地及德蘭修女等,亦是為自己尋求最大的利益。不過一般人心目中的『自己』,是小我,而偉人心目中的『自己』,是大我。可惜的是,無私並不一定是對,就像那些自殺式襲擊的人,當然是否偉大,便人言人殊。
說回「物競天擇」。其中一個結果是弱肉強食。如果最強的捕獵者也吃不了最弱的獵物,整個自然生態便會崩潰。美國某地方曾經有個以下的故事:為着保護純良的鹿,人類把凶殘的狼趕盡殺絕,然後失去天敵的鹿不受節制地繁殖,幾乎吃光了植物,所有的鹿差不多餓死,最後人類把狼從新引入,一切才回復平衝。
這個故事中,少數的生態學家對,多數的群眾錯。套用在人類社會。當我們實施一些措施時,我們是否真的明白後果?究竟要相信少數人的高瞻遠觸,還是多數人的集體智慧?
關鍵是教育:只有多數人都擁有知識,集體智慧才有意義。否則,不論是小數人獨裁,或多數人愚昧,都會導致災禍。
香港人的集體智慧,是否可以信賴?可以的話,香港就應該是民主政體、自由經濟。吊詭的是,有大商家反對民主,支持市場經濟;有社運人士支持民主,反對市場經濟;有左派說信賴群眾,但不支持民主,兼支持計劃經濟!
究意是甚麼回事?
當我們談及這三個槪念時,似乎經常出現邏輯矛盾:人是道的一部分,人的行為就是天的一部分,怎可以逆天而行?人是自然的一部分,人的行為就是自然的一部分,怎會是違反自然?人是市場的一部分,人的行為就是市場的一部分,怎可能叫作干預市場?
其實看深一層,是有點『成王敗寇』的味道。成功的,就是順應天命、符合自然、服從經濟規律;失敗的,就是逆天而行、破壞自然、搞亂市場運作。
究意有無客觀標準?只可以說,自古以來,人類都相信冥冥中萬物是跟從一定的模式運作。於是,我們憑着『成王敗寇』為例子,然後觀察、研究、學習,嘗試找出這個模式。
當我們掌握了一個模式,會利用它來為自己尋求更大的利益。不過,我們的模式可能是錯,或可能是對但出現不能控制的因素,但我們只能盡力而為--這個便是諺語「謀事在人,成事在天」,或更一般的,就是進化論中的「物競天擇」。
有人指出,為自己尋求最大的利益,是自私的行徑。但其實,聖雄甘地及德蘭修女等,亦是為自己尋求最大的利益。不過一般人心目中的『自己』,是小我,而偉人心目中的『自己』,是大我。可惜的是,無私並不一定是對,就像那些自殺式襲擊的人,當然是否偉大,便人言人殊。
說回「物競天擇」。其中一個結果是弱肉強食。如果最強的捕獵者也吃不了最弱的獵物,整個自然生態便會崩潰。美國某地方曾經有個以下的故事:為着保護純良的鹿,人類把凶殘的狼趕盡殺絕,然後失去天敵的鹿不受節制地繁殖,幾乎吃光了植物,所有的鹿差不多餓死,最後人類把狼從新引入,一切才回復平衝。
這個故事中,少數的生態學家對,多數的群眾錯。套用在人類社會。當我們實施一些措施時,我們是否真的明白後果?究竟要相信少數人的高瞻遠觸,還是多數人的集體智慧?
關鍵是教育:只有多數人都擁有知識,集體智慧才有意義。否則,不論是小數人獨裁,或多數人愚昧,都會導致災禍。
香港人的集體智慧,是否可以信賴?可以的話,香港就應該是民主政體、自由經濟。吊詭的是,有大商家反對民主,支持市場經濟;有社運人士支持民主,反對市場經濟;有左派說信賴群眾,但不支持民主,兼支持計劃經濟!
究意是甚麼回事?
Thursday, October 19, 2006
龐加箂之戰:數壇的天子
New York Times 似乎要和 The NewYorker 打對台,日前刊出了一篇題為The Emperor of Math 的文章,內對丘成桐有較為正面的描述。
文章內,丘成桐回應 The NewYorker 的 Manifold Destiny 把他妖魔化的陳述,否認貶低今屆菲爾茲奬(Fields Medal)得主對解決龐加箂猜想的頁獻。
其實龐加箂猜想的解決,應是數學界欣喜的事;現在卻變成錯綜複雜的恩恕情仇,令人不禁惋惜。
不過話說回來,New York Times 的觀點也不是一面倒。這篇文章的題目,給我的感覺是有點諷刺或嘲笑的意味,不知是否我太過敏感。
文章內,丘成桐回應 The NewYorker 的 Manifold Destiny 把他妖魔化的陳述,否認貶低今屆菲爾茲奬(Fields Medal)得主對解決龐加箂猜想的頁獻。
其實龐加箂猜想的解決,應是數學界欣喜的事;現在卻變成錯綜複雜的恩恕情仇,令人不禁惋惜。
不過話說回來,New York Times 的觀點也不是一面倒。這篇文章的題目,給我的感覺是有點諷刺或嘲笑的意味,不知是否我太過敏感。
Tuesday, October 03, 2006
純女性的國度
想像以下的國度:
一個純女性的國度,她們的祖先確是有男女兩性,但現在她們只倚靠自我細胞複製來繁殖下一代。
她們也有性行為,但這只是作為生理發泄,並沒有交換基因。
她們沒有一些成員扮演着男性,她們不需要這些。男性,只是存在於她們湮遠的回憶之中。
身為男性,對這個國度可能感到不安。不過,這個國度絕不是男性的地獄,因為這個國度根本沒有男性。我可不曉得這個國度會否是女性的天堂。
先不要對我所說的國度嗤之以鼻,以為痴人說夢,否則只顯出無知。這個國度,是真實存在的,她們就是新墨西哥鞭尾蜥(New Mexico Whiptail ,拉丁學名Cnemidophorus neomexicanus),是孤雌生殖(parthenogenic)的生物。
至於人類,可能將來有一批女性主義先鋒,駕着大空船,帶同最尖端的複製科技,在星際中建立一個心目中完美的新亞馬遜世界。
一個純女性的國度,她們的祖先確是有男女兩性,但現在她們只倚靠自我細胞複製來繁殖下一代。
她們也有性行為,但這只是作為生理發泄,並沒有交換基因。
她們沒有一些成員扮演着男性,她們不需要這些。男性,只是存在於她們湮遠的回憶之中。
身為男性,對這個國度可能感到不安。不過,這個國度絕不是男性的地獄,因為這個國度根本沒有男性。我可不曉得這個國度會否是女性的天堂。
先不要對我所說的國度嗤之以鼻,以為痴人說夢,否則只顯出無知。這個國度,是真實存在的,她們就是新墨西哥鞭尾蜥(New Mexico Whiptail ,拉丁學名Cnemidophorus neomexicanus),是孤雌生殖(parthenogenic)的生物。
至於人類,可能將來有一批女性主義先鋒,駕着大空船,帶同最尖端的複製科技,在星際中建立一個心目中完美的新亞馬遜世界。
Saturday, September 23, 2006
剎那的同時
剎那,佛家語,意指很短很短的時間。有計算是指大約13毫秒,或 1/75 秒。但若以其宗教意味來看,剎那其實近乎普朗克時間(Planck time)。
普朗克時間,大約5.4x10-44秒,是由上世紀初萌芽的量子力學--小尺度物理--的慨念。根據量子力學,普朗克時間是一個極限,即不能量度比它短的時間。既然如此,『同時』是甚麼意思?
另一套亦是由上世紀初萌芽的物理學,就是相對論--大尺度物理。根據這理論,信息傳播不能超越光速,因而不能另兩個計時器「真正」同步。亦即時間是相對的。那未『同時』又有甚麼意思?
把這兩套物理學融合為一,是現代物理學家的聖杯。霍金的《時間簡史》中的理論,亦以此聖杯為目的。
不過,霍金並未成功。反對其理論的物理學家,亦大有人在。連物理學家亦未能對時間的結構有一致意見,更不用說哲學家了。
建基於絕對時間,已經有不同的時間哲學。現在的情況,直是令人目眩!
愈看愈是胡塗。可能,時間根本是個『知得愈多,明得愈少』的玩意。
普朗克時間,大約5.4x10-44秒,是由上世紀初萌芽的量子力學--小尺度物理--的慨念。根據量子力學,普朗克時間是一個極限,即不能量度比它短的時間。既然如此,『同時』是甚麼意思?
另一套亦是由上世紀初萌芽的物理學,就是相對論--大尺度物理。根據這理論,信息傳播不能超越光速,因而不能另兩個計時器「真正」同步。亦即時間是相對的。那未『同時』又有甚麼意思?
把這兩套物理學融合為一,是現代物理學家的聖杯。霍金的《時間簡史》中的理論,亦以此聖杯為目的。
不過,霍金並未成功。反對其理論的物理學家,亦大有人在。連物理學家亦未能對時間的結構有一致意見,更不用說哲學家了。
建基於絕對時間,已經有不同的時間哲學。現在的情況,直是令人目眩!
愈看愈是胡塗。可能,時間根本是個『知得愈多,明得愈少』的玩意。
Thursday, September 21, 2006
龐加箂之戰:成桐反擊戰
今日《明報》分別有文章談及龐加箂之戰的兩位重要人物:丘成桐對中國學術界的批判,及Perelman的與世無爭。
不久前,NewYorker發表了一篇文章,提為Manifold Destiny。作者SYLVIA NASAR 及 DAVID GRUBER,把Perelman說成龐加箂之戰的隱士,而丘成桐則被描寫為歹角!
丘成桐當然不可以忍受如此侮辱,今週終於反擊!他發佈新聞稿,告訴傳媒他已向NewYorker發出律師信(Letter to New Yorker),要求正式報歉。
Manifold Destiny的作者,聽聞有意為龐加箂之戰出書及出劇本。但現在,他們亦為了故事中的人物。
正如我在http://wshun.blogspot.com/2006/08/new-yorker.html所說,一切 to be continued...
不久前,NewYorker發表了一篇文章,提為Manifold Destiny。作者SYLVIA NASAR 及 DAVID GRUBER,把Perelman說成龐加箂之戰的隱士,而丘成桐則被描寫為歹角!
丘成桐當然不可以忍受如此侮辱,今週終於反擊!他發佈新聞稿,告訴傳媒他已向NewYorker發出律師信(Letter to New Yorker),要求正式報歉。
Manifold Destiny的作者,聽聞有意為龐加箂之戰出書及出劇本。但現在,他們亦為了故事中的人物。
正如我在http://wshun.blogspot.com/2006/08/new-yorker.html所說,一切 to be continued...
Wednesday, September 20, 2006
圍棋與蒙地卡蘿
圍棋是中國國粹,亦是韓國及日本的受歡迎智力遊戲。下棋者,要計算每一步,不可存在撓倖之心。
根據數學理論,所有不含隨機成份的二人博奕,其中一方會有策略,可立於不敗之地。若然我們知道此策略,棋局未開始,便勝負已分。圍棋,沒有人知道這個策略,數學家才剛開始研究這個遊戲,亦因而衍生了相關的遊戲埋論。
蒙地卡蘿,世界著名賭城,每日有多少人在那搏一搏?運氣,在此可謂是必不可小的。
但利用統計學,或者可以增加勝算。蒙地卡蘿方法,是統計學上一個計算或然率的方法。
雖然我們不知道圍棋的必勝策略,但利用蒙地卡蘿方法,我們還是可以估計出每一步可能的最佳行法。這就是近年最新電腦圍棋程式的方向。
最近,wired有一篇訪問冠軍程式Crazy Stone的設計者Rémi Coulom的文章:
AI Invades Go Territory
裡面提到,他設計程式的目的是要贏其他電腦,不是要贏人,也不是要贏得漂亮。說得也是,用統計得來的步法,通常都是平淡,沒啥驚喜,有說棋手通常不大愛觀看這樣的棋局。
現在的電腦程式,已可以擊敗國際象棋世界冠軍。但電腦圍棋,連低段棋士也未能勝過。圍棋,是未來人工智能的新方向。
根據數學理論,所有不含隨機成份的二人博奕,其中一方會有策略,可立於不敗之地。若然我們知道此策略,棋局未開始,便勝負已分。圍棋,沒有人知道這個策略,數學家才剛開始研究這個遊戲,亦因而衍生了相關的遊戲埋論。
蒙地卡蘿,世界著名賭城,每日有多少人在那搏一搏?運氣,在此可謂是必不可小的。
但利用統計學,或者可以增加勝算。蒙地卡蘿方法,是統計學上一個計算或然率的方法。
雖然我們不知道圍棋的必勝策略,但利用蒙地卡蘿方法,我們還是可以估計出每一步可能的最佳行法。這就是近年最新電腦圍棋程式的方向。
最近,wired有一篇訪問冠軍程式Crazy Stone的設計者Rémi Coulom的文章:
AI Invades Go Territory
裡面提到,他設計程式的目的是要贏其他電腦,不是要贏人,也不是要贏得漂亮。說得也是,用統計得來的步法,通常都是平淡,沒啥驚喜,有說棋手通常不大愛觀看這樣的棋局。
現在的電腦程式,已可以擊敗國際象棋世界冠軍。但電腦圍棋,連低段棋士也未能勝過。圍棋,是未來人工智能的新方向。
Thursday, August 24, 2006
龐加箂之戰:The New Yorker
在前篇《龐加箂之戰》文中,我預告有人已為此撰文。估不到這麼快便出手了, SYLVIA NASAR (The Beautiful Mind 的作者)及 DAVID GRUBER 的
Manifold Destiny
正是為此數學界的大事作了較深入的報導。可惜的是,這個故事的歹角以乎是香港人,唉!
對我前篇不欣賞的人,希望這篇高水平的文章可以滿足他們的要求。戰鬥還未完結,還有一些枝節亦未在文章討論,所以 to be continued...
Manifold Destiny
正是為此數學界的大事作了較深入的報導。可惜的是,這個故事的歹角以乎是香港人,唉!
對我前篇不欣賞的人,希望這篇高水平的文章可以滿足他們的要求。戰鬥還未完結,還有一些枝節亦未在文章討論,所以 to be continued...
Monday, August 21, 2006
甚麼是normal?
A:如果獨身的人要收養孩子...
B:沒有國家容許獨身的人收養孩子!
C:因為要保證孩子有個normal family。
A:我可是個normal family專家啊。
要明白這個笑語(或者不太好笑),就要明白normal family的意思。第一個是指『正常的家庭』,後一個是數學上的『正規族』。
normal 這字,用途太廣範。
最原始的解釋,是指『理當如此』,如:A normal mother should love her children (正常的媽媽要受惜自己的兒女);或是指『多數如此』,如:A normal person could not run that fast(一般人不可能跑得這麼快』
然後,在社會學上,變成『與不平均數相距不遠』。這是把『多數如此』給出一個較準確的科學定義。不過,常用平均數有三,分別是眾數mode,均值mean,及中位數medium。若三者相若,則問題不大;但若三者相差頗大,用不同的平均數可能會做成爭議,猶其是用以制定政策時。
有一種統計學上的分佈方式,眾數、均值、中位數皆同,且越遠離平均數,越是罕有。這特殊的分佈稱為正態分佈normal distribution。若一個社會,它的財富是正態分佈,則窮人及富人都較罕有,反而是中產的較多,它的財富分佈會較為平均。所以,normal distribution的normal,是有點『理當如此』的意味。現實中,很少有真正的normal distribution,頂多是接近。所以,normal distribution並不是『多數如此』的distribution。
normal distribution是有很多優美的數學特性的distribution。很多不同的數學物件,都會有一些被稱為normal(中文稱為正規)的,是命名的數學家認為它的特性優美。除前述的normal family外,還有normal subgroup,normal matrix,諸如此類。這些normal的東西,一般非但不是『多數如此』,甚至乎相對罕有。
可以見到,笑話中的兩個normal,某方面的意義是完全相反!
B:沒有國家容許獨身的人收養孩子!
C:因為要保證孩子有個normal family。
A:我可是個normal family專家啊。
要明白這個笑語(或者不太好笑),就要明白normal family的意思。第一個是指『正常的家庭』,後一個是數學上的『正規族』。
normal 這字,用途太廣範。
最原始的解釋,是指『理當如此』,如:A normal mother should love her children (正常的媽媽要受惜自己的兒女);或是指『多數如此』,如:A normal person could not run that fast(一般人不可能跑得這麼快』
然後,在社會學上,變成『與不平均數相距不遠』。這是把『多數如此』給出一個較準確的科學定義。不過,常用平均數有三,分別是眾數mode,均值mean,及中位數medium。若三者相若,則問題不大;但若三者相差頗大,用不同的平均數可能會做成爭議,猶其是用以制定政策時。
有一種統計學上的分佈方式,眾數、均值、中位數皆同,且越遠離平均數,越是罕有。這特殊的分佈稱為正態分佈normal distribution。若一個社會,它的財富是正態分佈,則窮人及富人都較罕有,反而是中產的較多,它的財富分佈會較為平均。所以,normal distribution的normal,是有點『理當如此』的意味。現實中,很少有真正的normal distribution,頂多是接近。所以,normal distribution並不是『多數如此』的distribution。
normal distribution是有很多優美的數學特性的distribution。很多不同的數學物件,都會有一些被稱為normal(中文稱為正規)的,是命名的數學家認為它的特性優美。除前述的normal family外,還有normal subgroup,normal matrix,諸如此類。這些normal的東西,一般非但不是『多數如此』,甚至乎相對罕有。
可以見到,笑話中的兩個normal,某方面的意義是完全相反!
Wednesday, August 16, 2006
龐加箂之戰:粗疏的簡介
小道消息,有一些人已經磨拳擦掌,準備為世上少見的學術界比拼寫成小說。
真的,關於龐加箂猜想的歷史,簡直就是一部武俠小說。
龐加箂猜想,由Henri Poincaré於1904年提出。它的證明,就像一部人人這得到的武林秘笈。
然後,不斷有人嘗試證明。世人一步步接近這部秘笈。
Richard Hamilton提出一個大方向,公認是尋找秘笈的正確路向。
2000年,Clay Mathematics Institute宣佈,得到秘笈者將獲百萬美元奬金。
突然,一個隱士Grigori Perelman平空而出,宣稱已證明了龐加箂猜想。而然,因為他淡薄名利,恃世獨行,決不正式向武林公告,留下了不少問號。他現在已不知所踪(消息終於在今天明報刊登)。
既然留有問號,很多人仍然為這秘笈努力。三路人馬,皆要稱王。三路人馬分別是:曹懷東和朱熹平由丘成桐支持之下,宣佈正式解決了龐加箂猜想;耶魯大學的Bruce Kleiner與密歇根大學的 John Lott (University of Michigan);還有,南京大學的田剛與哥倫大學的 John Morgan。
田剛與丘成桐的師徒反目,田剛丘成桐事件為這場戰伇增添不少色彩。
還有不小有趣事件,恕未能在此披露。
真的,關於龐加箂猜想的歷史,簡直就是一部武俠小說。
龐加箂猜想,由Henri Poincaré於1904年提出。它的證明,就像一部人人這得到的武林秘笈。
然後,不斷有人嘗試證明。世人一步步接近這部秘笈。
Richard Hamilton提出一個大方向,公認是尋找秘笈的正確路向。
2000年,Clay Mathematics Institute宣佈,得到秘笈者將獲百萬美元奬金。
突然,一個隱士Grigori Perelman平空而出,宣稱已證明了龐加箂猜想。而然,因為他淡薄名利,恃世獨行,決不正式向武林公告,留下了不少問號。他現在已不知所踪(消息終於在今天明報刊登)。
既然留有問號,很多人仍然為這秘笈努力。三路人馬,皆要稱王。三路人馬分別是:曹懷東和朱熹平由丘成桐支持之下,宣佈正式解決了龐加箂猜想;耶魯大學的Bruce Kleiner與密歇根大學的 John Lott (University of Michigan);還有,南京大學的田剛與哥倫大學的 John Morgan。
田剛與丘成桐的師徒反目,田剛丘成桐事件為這場戰伇增添不少色彩。
還有不小有趣事件,恕未能在此披露。
Wednesday, August 09, 2006
The Joy Of Pi
Sunday, July 30, 2006
權力的量化
A:曾蔭權的權力有多大?
B:不大,他在立法局沒票。不小,他有保皇黨支持。
A:給我一個科學化的答案罷!
B:你是要一個數字?你是要一個可以代表權力大小的數字?
A:是啊。要投資也要知道風險系數嘛!
B:那就用權力指數罷。這是把權力量化的工具。
A:那挺不錯。
B:最常用的是Shapley-Shubik指數,美國總統擁有國會16%權力。
A:那美國國會是頗平衡的啊!
B:次常用的是Banzhaf指數,美國總統擁有國會4%權力。
A:這樣不成了破腳鴨總統嗎?
B:也有Johnson指數,美國總統擁有國會77%權力。
A:原來美國也是個獨裁政體!
B:最後是Deegan-Packel指數,美國總統擁有國會0.4%權力。
A:即是幾乎全無影嚮力?!
B:這純粹從制度計算,還未考慮政黨背景。
A:四種指數,差異真大!
B:若總統權力絕對大於議員,所有總統權力指數都大於議員。
A:所以計算的結果是,制度上,美國總統權力未必大於議員!
B:政治現實是,美國總統很少孤軍作戰,他的權力指數隨國會成份而變。
A:四種指數,孰優孰劣?
B:各有優勝處,各有吊詭處。
A:曾蔭權的權力有多大?
B:未計!
B:不大,他在立法局沒票。不小,他有保皇黨支持。
A:給我一個科學化的答案罷!
B:你是要一個數字?你是要一個可以代表權力大小的數字?
A:是啊。要投資也要知道風險系數嘛!
B:那就用權力指數罷。這是把權力量化的工具。
A:那挺不錯。
B:最常用的是Shapley-Shubik指數,美國總統擁有國會16%權力。
A:那美國國會是頗平衡的啊!
B:次常用的是Banzhaf指數,美國總統擁有國會4%權力。
A:這樣不成了破腳鴨總統嗎?
B:也有Johnson指數,美國總統擁有國會77%權力。
A:原來美國也是個獨裁政體!
B:最後是Deegan-Packel指數,美國總統擁有國會0.4%權力。
A:即是幾乎全無影嚮力?!
B:這純粹從制度計算,還未考慮政黨背景。
A:四種指數,差異真大!
B:若總統權力絕對大於議員,所有總統權力指數都大於議員。
A:所以計算的結果是,制度上,美國總統權力未必大於議員!
B:政治現實是,美國總統很少孤軍作戰,他的權力指數隨國會成份而變。
A:四種指數,孰優孰劣?
B:各有優勝處,各有吊詭處。
A:曾蔭權的權力有多大?
B:未計!
Thursday, July 27, 2006
立法會投票制度的維數
在香港,念數學而參與政治的名人,如今只有曾鈺成。但不知曾某對政治數學有多大研究?
政治數學,可以歸納為博奕論的一個分支,但絕非只是很多香港人自以為明白的納殊博奕。這裡我想一說,比較少人提及,立法會投票制度的數學模型。
為着簡化討論,我們不容許棄權票,即所有棄權票作反對票處理。
最簡單的立法會,是一人一票的簡單大多數。稍為複雜的,是『加權投票系統』(weighted voting system):即是在議會內,各位議員擁有可能不相同的票數,而議案通過的條件是要有超過預設數量的支持票。
舉例,有四人議會,一人有兩票,一人有三票,另兩人各有一票,議案雖四票支持才能通過。這就是『加權投票系統』,記作 [2,3,1,1;4]。
在幾乎大多數國家,都是用單一議會的加權投票系統。
數學上,我們稱這個為一維投票系統。即有一維,自然有二維。一個二維投票系統,是指議案要經過兩次不同的加權投票系統通過。
美國國會當然是二維,因為法案要分別通過參議院及眾議院。英國國會是雙議會制,但基本上議案只需在下議會通過,所以仍算是一維。
加拿大修改憲法,要多個一半省份支持,而支持省份要代表超過一半國民,才可通過。這是個二維系統。
一個n維投票系統,是指議案要經過n次不同的加權投票系統通過。
香 港立法會,政府議案通過只要多過一半議員支持,似乎是個一維;私人動議卻要功能議席及直選議席各有超過一半支持,似乎是個二維。加起來,香港立法會是個三 維投票系統!避開數學細節,計算時我們需要引入一位只會支持政府議案的隱形議員,他代表着香港政府在立法會內的直接影嚮力。
這些投票模型,可以幫助計算不同人或政黨的權力,亦可以幫助電腦模擬分析。
順帶提出,表面不相干的兩個學科,政治與數學,也可以有一定程度的連系。未來中學通識課程,為何可以被任意割裂?這真是通識嗎?
進介參考書:Alan D. Taylor, 《Mathematics and Politics》
政治數學,可以歸納為博奕論的一個分支,但絕非只是很多香港人自以為明白的納殊博奕。這裡我想一說,比較少人提及,立法會投票制度的數學模型。
為着簡化討論,我們不容許棄權票,即所有棄權票作反對票處理。
最簡單的立法會,是一人一票的簡單大多數。稍為複雜的,是『加權投票系統』(weighted voting system):即是在議會內,各位議員擁有可能不相同的票數,而議案通過的條件是要有超過預設數量的支持票。
舉例,有四人議會,一人有兩票,一人有三票,另兩人各有一票,議案雖四票支持才能通過。這就是『加權投票系統』,記作 [2,3,1,1;4]。
在幾乎大多數國家,都是用單一議會的加權投票系統。
數學上,我們稱這個為一維投票系統。即有一維,自然有二維。一個二維投票系統,是指議案要經過兩次不同的加權投票系統通過。
美國國會當然是二維,因為法案要分別通過參議院及眾議院。英國國會是雙議會制,但基本上議案只需在下議會通過,所以仍算是一維。
加拿大修改憲法,要多個一半省份支持,而支持省份要代表超過一半國民,才可通過。這是個二維系統。
一個n維投票系統,是指議案要經過n次不同的加權投票系統通過。
香 港立法會,政府議案通過只要多過一半議員支持,似乎是個一維;私人動議卻要功能議席及直選議席各有超過一半支持,似乎是個二維。加起來,香港立法會是個三 維投票系統!避開數學細節,計算時我們需要引入一位只會支持政府議案的隱形議員,他代表着香港政府在立法會內的直接影嚮力。
這些投票模型,可以幫助計算不同人或政黨的權力,亦可以幫助電腦模擬分析。
順帶提出,表面不相干的兩個學科,政治與數學,也可以有一定程度的連系。未來中學通識課程,為何可以被任意割裂?這真是通識嗎?
進介參考書:Alan D. Taylor, 《Mathematics and Politics》
Thursday, July 20, 2006
吸血蟲的強暴世界
我一向相信,所有人的行為都可在其他生物找到。一些人類的邪惡行為,可能是某些生物的正常生活。
吸血蟲begbug的世界內,所有的性行為都可稱為強姦。雄蟲在交配時,針狀的生殖器直接插穿雌蟲表面進入體內。因而雌蟲表面可以見到一個個孔洞。
其他的昆蟲,雄性要先得雌性歡心,然後用生殖器對生殖器,把精子送入。吸血蟲的雄蟲一於拳頭至上,覇王硬上弓,連對方生殖器入口也不找了,索性隨意插入!
生物學家說,這是吸血蟲的進化策略,減少求偶所需的虛耗。噢!
吸血蟲的世界內,還有雄性姦雄性!當強者面對弱者,會毫不留情的施暴!這行為的原因,生物學家還在搔不着頭腦。
有一種說法,是施暴者在受害者體內留下精子,在受害者與異性接觸時,會把施暴者的精子一拼射出。若如是,則受害者還要幫助施暴者傳宗接代!可能是自然間最邪惡的雄性姦雄性了。
不過生物學家說這猜測還找不到證據。
吸血蟲begbug的世界內,所有的性行為都可稱為強姦。雄蟲在交配時,針狀的生殖器直接插穿雌蟲表面進入體內。因而雌蟲表面可以見到一個個孔洞。
其他的昆蟲,雄性要先得雌性歡心,然後用生殖器對生殖器,把精子送入。吸血蟲的雄蟲一於拳頭至上,覇王硬上弓,連對方生殖器入口也不找了,索性隨意插入!
生物學家說,這是吸血蟲的進化策略,減少求偶所需的虛耗。噢!
吸血蟲的世界內,還有雄性姦雄性!當強者面對弱者,會毫不留情的施暴!這行為的原因,生物學家還在搔不着頭腦。
有一種說法,是施暴者在受害者體內留下精子,在受害者與異性接觸時,會把施暴者的精子一拼射出。若如是,則受害者還要幫助施暴者傳宗接代!可能是自然間最邪惡的雄性姦雄性了。
不過生物學家說這猜測還找不到證據。
Monday, July 17, 2006
七種『母親』
近來有幾位朋友剛為人母,或將為人母。剛好近期又讀到一些花邊新聞,便寫寫不同種類的 『母親』:生母,代母,飬母,後母,契母,教母,師母。
通常只有前四種可被稱為母親,但後三者確分擔一部分母親的職責,故一拼論之。
若徒兒的師父為男性,徒兒師父的妻子便稱為徒兒的師母。恕我如此累贅,因我想順勢提出,若徒兒的師父為女性,徒兒師父的丈夫卻沒有特別稱呼!
師母與徒兒的關係,要視乎她對丈夫事業的介入度有關。這關係會非常疏離,但在一些傳統的行業,可能師母也負着一些教飬的責任。
教母,好像是天主教獨有:每位教徒都有一位教母,為孩子給與一些宗教上或生活上的幫助。契母,是中國民間的傳統:當二人建立了契約的關係,契母便有責任給契子女給與一些道德上或生活上的指引。教母與契母,在傳統的天主教家庭,幾乎沒有分別。
當然,每個天主教徒都有一位亦只有一位教母,但一個中國人可以沒有或有多於一位契母。
後母,是指父親再娶的妻子。這個不用多說。
真正飬育孩子的女人,就是飬母。對飬母不是生母的人,可能有「生娘不及飬娘大」之嘆。
有一種界乎生母與飬母之間的,就是古時大戶人家的乳娘。這種要放棄用自己的奶餵餔自己孩子的古老職業,聽說最近在中國大陸再次出現。可能是因為現代醫學界重新提倡母乳比奶粉好。
生母是誰?如果你的答案是『生你下來的女人』,已跟不上時代。陸恭蕙的孩子,並非她生下來的,而是請人代生的。用自己的卵子與丈夫的精子結合,放在另一個女人的子宫內,誔下自己的孩子。陸恭蕙才是那孩子的生母,供給子宫的女人便是孩子的代母。
十月懷胎的女人,竟然只是代母,而不是孩子的生母,這是對社會倫理的一大衝激。
那麼生母是否『卵子的供給者』?又不是這麼簡單。也有的不育妻子,讓他人的卵子與丈夫的精子結合,放入自己的子宫內。這在法律上,自己仍是孩子的生母,而卵子的供給者仍只是卵子的供給者!
科學家曾把兩個老鼠的卵子結合成胚胎。如果人的卵子也可依樣胡蘆,那可知問題更大。
還記得阿諾舒華申力加的《龍兄鼠弟》嗎?主角是不同人基因的混合體,所以他有多個生父生母。但他還只有一個把他生下來的女人,而這女人便是後來與他團聚的母親。就現代法律來看,這是他的生母嗎?
通常只有前四種可被稱為母親,但後三者確分擔一部分母親的職責,故一拼論之。
若徒兒的師父為男性,徒兒師父的妻子便稱為徒兒的師母。恕我如此累贅,因我想順勢提出,若徒兒的師父為女性,徒兒師父的丈夫卻沒有特別稱呼!
師母與徒兒的關係,要視乎她對丈夫事業的介入度有關。這關係會非常疏離,但在一些傳統的行業,可能師母也負着一些教飬的責任。
教母,好像是天主教獨有:每位教徒都有一位教母,為孩子給與一些宗教上或生活上的幫助。契母,是中國民間的傳統:當二人建立了契約的關係,契母便有責任給契子女給與一些道德上或生活上的指引。教母與契母,在傳統的天主教家庭,幾乎沒有分別。
當然,每個天主教徒都有一位亦只有一位教母,但一個中國人可以沒有或有多於一位契母。
後母,是指父親再娶的妻子。這個不用多說。
真正飬育孩子的女人,就是飬母。對飬母不是生母的人,可能有「生娘不及飬娘大」之嘆。
有一種界乎生母與飬母之間的,就是古時大戶人家的乳娘。這種要放棄用自己的奶餵餔自己孩子的古老職業,聽說最近在中國大陸再次出現。可能是因為現代醫學界重新提倡母乳比奶粉好。
生母是誰?如果你的答案是『生你下來的女人』,已跟不上時代。陸恭蕙的孩子,並非她生下來的,而是請人代生的。用自己的卵子與丈夫的精子結合,放在另一個女人的子宫內,誔下自己的孩子。陸恭蕙才是那孩子的生母,供給子宫的女人便是孩子的代母。
十月懷胎的女人,竟然只是代母,而不是孩子的生母,這是對社會倫理的一大衝激。
那麼生母是否『卵子的供給者』?又不是這麼簡單。也有的不育妻子,讓他人的卵子與丈夫的精子結合,放入自己的子宫內。這在法律上,自己仍是孩子的生母,而卵子的供給者仍只是卵子的供給者!
科學家曾把兩個老鼠的卵子結合成胚胎。如果人的卵子也可依樣胡蘆,那可知問題更大。
還記得阿諾舒華申力加的《龍兄鼠弟》嗎?主角是不同人基因的混合體,所以他有多個生父生母。但他還只有一個把他生下來的女人,而這女人便是後來與他團聚的母親。就現代法律來看,這是他的生母嗎?
Thursday, July 06, 2006
自由選舉及自由貿易
有人說:人有選擇管治者的自由
(有人說:人有選擇經濟活動的自由)
現實是:民主菲律賓經常政變,民主印度多數人生活艱苦
(現實是:自由貿易令美國工人失業,自由貿易令南韓農民生活艱苦)
歷史上:民主美國出現南北戰爭,民主菲律賓選出獨裁馬可斯
(歷史上:1860-1892歐洲對外貿易最少干預卻出現了著名的經濟大衰退,在 20世紀 60至 80年代美國大幅減少關稅的干預但平均經濟增長卻低)
所以,人權分子說民主有益於國民並不一定成立
(所以,經濟學家說自由貿易有利於國民並不一定成立)
我們不應盲目相信民主
(我們不應盲目相信自由貿易)
結論是:國情不同,民主不適合我們
(結論是:國情不同,自由貿易不適合我們)
結論是:在國民不成熟時,不應倉卒推行民主,我們要遁序漸進,最終會達至民主的
(結論是:在國民未準備好時,不應倉卒開放市場,我們要遁序漸進,最終會達至自由貿易)
(有人說:人有選擇經濟活動的自由)
現實是:民主菲律賓經常政變,民主印度多數人生活艱苦
(現實是:自由貿易令美國工人失業,自由貿易令南韓農民生活艱苦)
歷史上:民主美國出現南北戰爭,民主菲律賓選出獨裁馬可斯
(歷史上:1860-1892歐洲對外貿易最少干預卻出現了著名的經濟大衰退,在 20世紀 60至 80年代美國大幅減少關稅的干預但平均經濟增長卻低)
所以,人權分子說民主有益於國民並不一定成立
(所以,經濟學家說自由貿易有利於國民並不一定成立)
我們不應盲目相信民主
(我們不應盲目相信自由貿易)
結論是:國情不同,民主不適合我們
(結論是:國情不同,自由貿易不適合我們)
結論是:在國民不成熟時,不應倉卒推行民主,我們要遁序漸進,最終會達至民主的
(結論是:在國民未準備好時,不應倉卒開放市場,我們要遁序漸進,最終會達至自由貿易)
Monday, June 26, 2006
風俗的演化
隨着支持種族主義的達爾文社會論(Social Darwinism)被掃入垃圾堆,演化論在社會學的真正用處開始浮現。演化論逐漸成為不同人文學科的共同語言。
演化論說:『畸胎』年年有,但往往不能存活。不過可能因緣際會,例如環境突變,生存下來並留有後代,一個新物種因而誔生。令一方面,原來的物種有可能適應不了變化,終至消亡。
同理:『古靈精怪想法』人人有,但往往不能付諸實行。不過可能因緣際會,想法得到落實,甚至變成代代相傳的習慣,一個新風俗因而誔生。令一方面,原來的風俗有可能適應不了變化,終至消亡。
畸胎的出現,可能是自然突變,可能是幅射化學干涉,也可能是被其他生物(人或細箘)的影嚮。
一種想法的出現,可能純是胡思亂想,可能是希望消災解刼,也可能是被其他外力所影嚮。
一個出名卻不知出處的『五實驗』故事,見〔1〕〔2〕,簡述如下:
又如扎腳,最初是某皇帝對小腳的畸型愛好。上行下效之後,演變成貴婦的象徵。滿清曾明令禁止,但對貴婦形象的偏好,使禁令形同虛設。及至列強入侵,騎在中國人頭上的外國貴婦不需扎腳,扎腳的形象直插谷底。
泰北某小數民族,女子以長頸為美。估計起因也和扎腳差不多,對身體也做成損害。為甚麼這習俗沒有消失?族內的人美其名曰保留傳統,事實是把女人作為新一代搖錢樹,吸引遊客。喜歡獵奇的遊客,是否也有責任?!
美國的黑奴制度,起點是把非洲人作廉價勞工。但隨着黑人落地生根,世代繁衍,黑人白人都出現兩極情況。某些白人發覺把黑人看作僱員,比把他們看作奴隸(要 提供食宿)化算,某些白人仍然相信奴隸制是個理想制度;某些黑人渴望獲得自由,某些黑人卻害怕生活改變。結果是南北戰爭。
現在的減肥狂潮,起因是肥胖有損建康,醫學界提倡;繼而做生意的看見商機,把這個主導權搶過來;最後是女人自我設限,比男人所設的標準更為苛刻。這也是個不合理的風俗,也不知會如何結束。
演化論說:『畸胎』年年有,但往往不能存活。不過可能因緣際會,例如環境突變,生存下來並留有後代,一個新物種因而誔生。令一方面,原來的物種有可能適應不了變化,終至消亡。
同理:『古靈精怪想法』人人有,但往往不能付諸實行。不過可能因緣際會,想法得到落實,甚至變成代代相傳的習慣,一個新風俗因而誔生。令一方面,原來的風俗有可能適應不了變化,終至消亡。
畸胎的出現,可能是自然突變,可能是幅射化學干涉,也可能是被其他生物(人或細箘)的影嚮。
一種想法的出現,可能純是胡思亂想,可能是希望消災解刼,也可能是被其他外力所影嚮。
一個出名卻不知出處的『五實驗』故事,見〔1〕〔2〕,簡述如下:
有五隻子困在籠內,某角落有隻香蕉。誰有膽走近香蕉,所有子都被水淋。久而久之,沒子敢接近香蕉。
接着,換入一隻新子,當它欲接近香蕉時,被其他不想被水淋的子群起而攻之。它不明所以,只知接近香蕉者該打!
最後,所有舊子被掉走了,但新子認為接近香蕉者該打。香蕉已成禁忌。
其實,科學家早決定不再淋水,剩下來的只是無聊的禁忌。
一天這禁忌不影嚮子的生計,一天它們也不會去挑戰這禁忌。除非一日有重大改變,例如有隻不怕打的子敢去取香蕉,一日這禁忌仍然存在!
譬如避諱,是避免名字相同引起混亂。及後變成下級改名遷就上級,進而達至「只許州官放火,不許百姓點燈」的荒謬。最後是封建制度崩潰,連避諱也一拼消失。接着,換入一隻新子,當它欲接近香蕉時,被其他不想被水淋的子群起而攻之。它不明所以,只知接近香蕉者該打!
最後,所有舊子被掉走了,但新子認為接近香蕉者該打。香蕉已成禁忌。
其實,科學家早決定不再淋水,剩下來的只是無聊的禁忌。
一天這禁忌不影嚮子的生計,一天它們也不會去挑戰這禁忌。除非一日有重大改變,例如有隻不怕打的子敢去取香蕉,一日這禁忌仍然存在!
又如扎腳,最初是某皇帝對小腳的畸型愛好。上行下效之後,演變成貴婦的象徵。滿清曾明令禁止,但對貴婦形象的偏好,使禁令形同虛設。及至列強入侵,騎在中國人頭上的外國貴婦不需扎腳,扎腳的形象直插谷底。
泰北某小數民族,女子以長頸為美。估計起因也和扎腳差不多,對身體也做成損害。為甚麼這習俗沒有消失?族內的人美其名曰保留傳統,事實是把女人作為新一代搖錢樹,吸引遊客。喜歡獵奇的遊客,是否也有責任?!
美國的黑奴制度,起點是把非洲人作廉價勞工。但隨着黑人落地生根,世代繁衍,黑人白人都出現兩極情況。某些白人發覺把黑人看作僱員,比把他們看作奴隸(要 提供食宿)化算,某些白人仍然相信奴隸制是個理想制度;某些黑人渴望獲得自由,某些黑人卻害怕生活改變。結果是南北戰爭。
現在的減肥狂潮,起因是肥胖有損建康,醫學界提倡;繼而做生意的看見商機,把這個主導權搶過來;最後是女人自我設限,比男人所設的標準更為苛刻。這也是個不合理的風俗,也不知會如何結束。
Wednesday, June 21, 2006
食肉的素食者?
閣下為何選擇吃素?若是宗教原因,以下的文章可能與你有關:
Test Tube Meat Nears Dinner Table
利用實驗室人工培殖肉塊,吃它還算不算吃素?
記得多年前肯德基不再「家鄉雞」時,有傳言「肯德基不是雞」。當時我與一位信佛朋友討論,他笑說這樣他便有雞吃了。
其實在很多科幻電影中,人工合成肉類早不是新鮮事兒。不過今天的新聞,是把小說變成事實再跨出一步。
對香港人來說,人工培殖軟骨可能更具吸引力。醫學上,人工軟骨有極大用途,但我不是說這個。對嗜翅成性的港人,人工培殖魚翅是個好東西,畢竟市面假翅充斥,且捕鯊有道德問題。
我知有很多機構在研究人工軟骨,為何沒有人工魚翅呢?
Test Tube Meat Nears Dinner Table
利用實驗室人工培殖肉塊,吃它還算不算吃素?
記得多年前肯德基不再「家鄉雞」時,有傳言「肯德基不是雞」。當時我與一位信佛朋友討論,他笑說這樣他便有雞吃了。
其實在很多科幻電影中,人工合成肉類早不是新鮮事兒。不過今天的新聞,是把小說變成事實再跨出一步。
對香港人來說,人工培殖軟骨可能更具吸引力。醫學上,人工軟骨有極大用途,但我不是說這個。對嗜翅成性的港人,人工培殖魚翅是個好東西,畢竟市面假翅充斥,且捕鯊有道德問題。
我知有很多機構在研究人工軟骨,為何沒有人工魚翅呢?
Monday, June 19, 2006
一則科幻小說:誰是母親?
某年某月某日,某間空置已久的工廠突然傳出巨響。人們驚訝發現,內裡有一個不知從何而來,卻已燒壞的機器,旁邊是一個剛滿月的女嬰。
女嬰被收養,長大後成為出色的科學家,參與了兩項極具爭議的研究。首先,她把自己的細胞變成胚胎,放在自己的子宮內繁殖,誕下複製了的自己;其次,她決定要製造時間機器,地點是她當年被發現的地方,當時仍被空置的工廠。
這天,她帶着自己的複製品,來到工廠。她把女嬰放在時間機器一旁,然後測試電腦的數據。不知怎地,時間機器突然發動,產生的波動把周遭的都吸去。科學家僥倖避過了,但女嬰及時間機器卻失去了!
科學家終於知道誰是自己的母親,但卻仍然不知道自己從何而來!
***********
Robert A. Heinlein的"--All Your Zombies--" 太過複雜了。以上是個沒有男女關係的簡化版。
女嬰被收養,長大後成為出色的科學家,參與了兩項極具爭議的研究。首先,她把自己的細胞變成胚胎,放在自己的子宮內繁殖,誕下複製了的自己;其次,她決定要製造時間機器,地點是她當年被發現的地方,當時仍被空置的工廠。
這天,她帶着自己的複製品,來到工廠。她把女嬰放在時間機器一旁,然後測試電腦的數據。不知怎地,時間機器突然發動,產生的波動把周遭的都吸去。科學家僥倖避過了,但女嬰及時間機器卻失去了!
科學家終於知道誰是自己的母親,但卻仍然不知道自己從何而來!
***********
Robert A. Heinlein的"--All Your Zombies--" 太過複雜了。以上是個沒有男女關係的簡化版。
Tuesday, June 13, 2006
能源與環保:永難共享?
紐約時報刊登了以下的文章:
Pollution From Chinese Coal Casts a Global Shadow
談的是燃煤發電在中國引起的經濟環保問題。
煤,是『廉價』能源。不甘花錢去買最新的燃煤發電設備,中國的煤發電效率最低,汚染最高--又一個短視的例子。但中國的汚染,已達至不容忽視的水平,迫得中國政府開始研究不同的能源。
石油,供應會受國際形勢影嚮,來源不隱,除非煤液化技術成功。但石油跟煤一樣,產生室溫氣體,令全球暖化。
核裂變,人為錯誤造成的核工廠意外,最令人害怕。即使是最新的技術,已是相當安全,但所產生的幅射廢料,長遠亦是隱患。
核聚變,有中國參與的首個大型電廠,將於法國興建。最大的批評是,投資具大卻未必有成果,不若把金錢投放在其他再生能源。
水力發電,需要人為改變生態環境,為害不用多說。
風力發電,亦被一些環保分子垢病,皆因誤撞風車而死的鳥兒,不計其數。
太陽能,被譽為最環保,可惜成本太貴且效率太低。而且,製造高質素太陽能發電板,亦可能需要對環境有害的物料。
好了,進入死胡同了!所有的方法都有環保理由去反對。怎麼辦?怎麼辦?
Pollution From Chinese Coal Casts a Global Shadow
談的是燃煤發電在中國引起的經濟環保問題。
煤,是『廉價』能源。不甘花錢去買最新的燃煤發電設備,中國的煤發電效率最低,汚染最高--又一個短視的例子。但中國的汚染,已達至不容忽視的水平,迫得中國政府開始研究不同的能源。
石油,供應會受國際形勢影嚮,來源不隱,除非煤液化技術成功。但石油跟煤一樣,產生室溫氣體,令全球暖化。
核裂變,人為錯誤造成的核工廠意外,最令人害怕。即使是最新的技術,已是相當安全,但所產生的幅射廢料,長遠亦是隱患。
核聚變,有中國參與的首個大型電廠,將於法國興建。最大的批評是,投資具大卻未必有成果,不若把金錢投放在其他再生能源。
水力發電,需要人為改變生態環境,為害不用多說。
風力發電,亦被一些環保分子垢病,皆因誤撞風車而死的鳥兒,不計其數。
太陽能,被譽為最環保,可惜成本太貴且效率太低。而且,製造高質素太陽能發電板,亦可能需要對環境有害的物料。
好了,進入死胡同了!所有的方法都有環保理由去反對。怎麼辦?怎麼辦?
Thursday, June 08, 2006
宣傳至上的龐加箂猜想證明
2006年6月3日,丘成桐宣佈:龐加萊猜想(The Poincaré Conjecture)最終由兩位中國數學家朱熹平和曹懷東證明了!
咪住,怎麼這件數學界大事只在中文報章大肆報道,而其他報章卻輕輕帶過,甚或隻字不提?當年安德魯·懷爾斯(Andrew Wiles)證明費馬大定理(Fermat's Last Theorem)不是在全世界引起轟動嗎?
是種族歧視嗎?他們妒忌中國人的成就?
都不是,原因是數學界一般同意,龐加箂猜想可能早於2002年由蘇聯人格裡戈里·佩雷爾曼(Григорий Яковлевич Перельман, Grigorii Yakovlevich Perelman)證明了,只是中間有的漏洞未完全堵塞。這猜想會於十年內正式解決,幾本已以乎已是共識!
龐加箂猜想是:『每一個沒有破洞的封閉三維物體,都等價於三維的球面。』由龐加萊(Henri Poincaré)於1904提出,突破口是Richard Hamilton在1966年的新數學方法,而佩雷爾曼在2002年加以改進。若朱曹二人當真為此平頂,會在世界數學史佔一席位,但其頁獻仍遜於前人。
相反懷爾斯確實作出突破,且是在沒有人預計情況下,宣報證明了費馬大定理。
既然朱曹二人只是為龐加箂猜想平頂,為何丘成桐會高調宣報?又為何中文報章會大肆報道?
首先,中國記者是善忘的,忘記了2002年報章曾廣泛報道佩雷爾曼可能證明了龐加箂猜想。
其次,中國人老想着要有中國人的成就,不求甚解的用上『中國人證明世紀數學難題』般的標題。
最後,丘成桐深明宣傳之道,懂得如何提高知名度。雖然香港各大學數學系研究及師資半斤八兩,但中文大學數學系的曝光率遙遙領先,與此不無關係。
忘記一提,若龐加箂猜想真的證明了,相關的克雷數學研究所(Clay Mathematics Institute,CMI)一百萬美元怎樣分派,倒令人迷惑。原因是該奬項規定得奬論文必要在數學期刊上發表,而佩雷爾曼是個自負且不好金錢的奇人,他的論文只是放在自已網頁上!但如果只是朱曹得奬,數學界應會群情淘湧!
咪住,怎麼這件數學界大事只在中文報章大肆報道,而其他報章卻輕輕帶過,甚或隻字不提?當年安德魯·懷爾斯(Andrew Wiles)證明費馬大定理(Fermat's Last Theorem)不是在全世界引起轟動嗎?
是種族歧視嗎?他們妒忌中國人的成就?
都不是,原因是數學界一般同意,龐加箂猜想可能早於2002年由蘇聯人格裡戈里·佩雷爾曼(Григорий Яковлевич Перельман, Grigorii Yakovlevich Perelman)證明了,只是中間有的漏洞未完全堵塞。這猜想會於十年內正式解決,幾本已以乎已是共識!
龐加箂猜想是:『每一個沒有破洞的封閉三維物體,都等價於三維的球面。』由龐加萊(Henri Poincaré)於1904提出,突破口是Richard Hamilton在1966年的新數學方法,而佩雷爾曼在2002年加以改進。若朱曹二人當真為此平頂,會在世界數學史佔一席位,但其頁獻仍遜於前人。
相反懷爾斯確實作出突破,且是在沒有人預計情況下,宣報證明了費馬大定理。
既然朱曹二人只是為龐加箂猜想平頂,為何丘成桐會高調宣報?又為何中文報章會大肆報道?
首先,中國記者是善忘的,忘記了2002年報章曾廣泛報道佩雷爾曼可能證明了龐加箂猜想。
其次,中國人老想着要有中國人的成就,不求甚解的用上『中國人證明世紀數學難題』般的標題。
最後,丘成桐深明宣傳之道,懂得如何提高知名度。雖然香港各大學數學系研究及師資半斤八兩,但中文大學數學系的曝光率遙遙領先,與此不無關係。
忘記一提,若龐加箂猜想真的證明了,相關的克雷數學研究所(Clay Mathematics Institute,CMI)一百萬美元怎樣分派,倒令人迷惑。原因是該奬項規定得奬論文必要在數學期刊上發表,而佩雷爾曼是個自負且不好金錢的奇人,他的論文只是放在自已網頁上!但如果只是朱曹得奬,數學界應會群情淘湧!
Wednesday, June 07, 2006
婚姻的意義
有朋友說:以經濟學角度,一夫多妻是最好的。也有朋友說:一夫一妻是最文明的。不論如何,其實一夫多妻、一妻多夫、甚或同性婚姻,廣義上在香港是『合法』的。
此話怎說?香港法律規定:每人只可與一位異性註冊結婚;若多於一位,便犯重婚罪。但若有人選擇『不註冊婚姻』 ,倒不是犯法。最出名的有何鴻桑的多位太太。筆者也認識一對結婚多年,有兒有女的夫婦,最後是因要申請居屋才正式註冊!
這也是的,若由荷蘭來香港定居的同性配偶,或由中東搬來香港有四個太太的回教徒,倒不成說他們的婚姻不合法。當然囉,帶來的法律問題會是非常複雜。
要知道,香港是近四十年才切實執行一夫一妻制,之前只要是三書六禮,一個男人的所有妻子都受法律保障。基督教是一夫一妻制的,但舊約時也是一夫多妻的。中世紀時,有些君主需已接受基督教,但仍以延續王室血脈為由納妾。現在據稱還有一妻多夫的小數民族。可以說,一種婚姻受法律認可,其實是反映當時的社會需要。
論結婚對象的選擇,遠古時的男女雜交選擇最多,但這不利於社會穩定。
一夫多妻制,女的可以選擇己婚男性作對象,以此角度看,是比較一夫一妻制優勝。怪不得會成為古代大多數社會的主流。
然而,隨着男女地位變得平等,與人分享配偶亦變得不可接受,一夫一妻制遂在現代社會生根。
婚姻的定義,隨社會變遷而改變。但最簡單的是,一男一女互相照顧的契約。在傳統的社會內,男的工作飬家、女的持家有道、再加上生兒育女,是婚姻的社會責任;若做不到,會承受巨大的社會壓力。選擇配偶的條件,會是門當戶對、好生飬、或合適的經濟政治背景。在父母之命,盲婚啞嫁的從前,戀愛可能是結婚之後的事。私定終身,其罪大焉!
今天的婚姻,和一百年前的婚姻,意義與社會功能已大不同。在標榜個人自由的今天,戀愛逐漸變成婚姻最重要的部分。亦正因如此,同性戀者認為法律上婚姻定義也應蓋涵男男或女女,這才是公平。但『同性婚姻』的概念從未在中國出現過,它究意是否婚姻,是定義問題。若大家認為同性婚姻不是婚姻,就不存在法律是否承認的問題。
現實有一男愛多女,或一女愛多男,為何法律上不能認可一夫多妻或一妻多夫呢?畢竟這在中國社會出現過。但既然在香港,法律上一夫一妻制幾乎是共識,亦因而沒有動力去改變婚姻的法律定義。
此話怎說?香港法律規定:每人只可與一位異性註冊結婚;若多於一位,便犯重婚罪。但若有人選擇『不註冊婚姻』 ,倒不是犯法。最出名的有何鴻桑的多位太太。筆者也認識一對結婚多年,有兒有女的夫婦,最後是因要申請居屋才正式註冊!
這也是的,若由荷蘭來香港定居的同性配偶,或由中東搬來香港有四個太太的回教徒,倒不成說他們的婚姻不合法。當然囉,帶來的法律問題會是非常複雜。
要知道,香港是近四十年才切實執行一夫一妻制,之前只要是三書六禮,一個男人的所有妻子都受法律保障。基督教是一夫一妻制的,但舊約時也是一夫多妻的。中世紀時,有些君主需已接受基督教,但仍以延續王室血脈為由納妾。現在據稱還有一妻多夫的小數民族。可以說,一種婚姻受法律認可,其實是反映當時的社會需要。
論結婚對象的選擇,遠古時的男女雜交選擇最多,但這不利於社會穩定。
一夫多妻制,女的可以選擇己婚男性作對象,以此角度看,是比較一夫一妻制優勝。怪不得會成為古代大多數社會的主流。
然而,隨着男女地位變得平等,與人分享配偶亦變得不可接受,一夫一妻制遂在現代社會生根。
婚姻的定義,隨社會變遷而改變。但最簡單的是,一男一女互相照顧的契約。在傳統的社會內,男的工作飬家、女的持家有道、再加上生兒育女,是婚姻的社會責任;若做不到,會承受巨大的社會壓力。選擇配偶的條件,會是門當戶對、好生飬、或合適的經濟政治背景。在父母之命,盲婚啞嫁的從前,戀愛可能是結婚之後的事。私定終身,其罪大焉!
今天的婚姻,和一百年前的婚姻,意義與社會功能已大不同。在標榜個人自由的今天,戀愛逐漸變成婚姻最重要的部分。亦正因如此,同性戀者認為法律上婚姻定義也應蓋涵男男或女女,這才是公平。但『同性婚姻』的概念從未在中國出現過,它究意是否婚姻,是定義問題。若大家認為同性婚姻不是婚姻,就不存在法律是否承認的問題。
現實有一男愛多女,或一女愛多男,為何法律上不能認可一夫多妻或一妻多夫呢?畢竟這在中國社會出現過。但既然在香港,法律上一夫一妻制幾乎是共識,亦因而沒有動力去改變婚姻的法律定義。
Saturday, June 03, 2006
由世界盃到演化論
相比起進化論,我較為喜歡用演化論。一般人喜愛把演化論歸納為『優勝劣敗』。
以狒狒為例,若某雄性狒狒成為王者,它可以獨攬所有的雌性狒狒。對這現象的解釋是,如此可確保最優秀的基因可延續下去。那末,勝出的是最優秀,敗陣的當然較劣等,不是嗎?
錯了!讓我先談談世界盃。在多國球隊中,只有一隊可以奪冠。香港、新加坡、汶箂等,是名副其實的弱旅,被淘汰是必然的;但巴西、阿根廷、英格蘭等頂級強隊,不能說巴西棒盃便代表巴西比阿根廷或英格蘭優秀!因為規矩是只有一隊冠軍,即使是同樣優良亦要分出勝負。正如一句老話:「波是圓的」,最後其實的運氣決定一切。
若世界盃的結果,是所有球隊學習冠軍的踢法,我們會見到一個沉悶的足球世界。同理,一夫多妻制的結果,是犧牲了基因多樣性,亦是個缺憾。
其實自然界中,除一夫多妻外,也有一妻多夫,一夫一妻及其他,每種都各有好壞。優勝劣敗根本是個過於簡單的描述。
或者,狒狒的一夫多妻其實衹是隨機的產物,誰知千萬年後,若不絕種的話,會否出現另外的社會模式?
以狒狒為例,若某雄性狒狒成為王者,它可以獨攬所有的雌性狒狒。對這現象的解釋是,如此可確保最優秀的基因可延續下去。那末,勝出的是最優秀,敗陣的當然較劣等,不是嗎?
錯了!讓我先談談世界盃。在多國球隊中,只有一隊可以奪冠。香港、新加坡、汶箂等,是名副其實的弱旅,被淘汰是必然的;但巴西、阿根廷、英格蘭等頂級強隊,不能說巴西棒盃便代表巴西比阿根廷或英格蘭優秀!因為規矩是只有一隊冠軍,即使是同樣優良亦要分出勝負。正如一句老話:「波是圓的」,最後其實的運氣決定一切。
若世界盃的結果,是所有球隊學習冠軍的踢法,我們會見到一個沉悶的足球世界。同理,一夫多妻制的結果,是犧牲了基因多樣性,亦是個缺憾。
其實自然界中,除一夫多妻外,也有一妻多夫,一夫一妻及其他,每種都各有好壞。優勝劣敗根本是個過於簡單的描述。
或者,狒狒的一夫多妻其實衹是隨機的產物,誰知千萬年後,若不絕種的話,會否出現另外的社會模式?
Tuesday, May 30, 2006
親疏如何有別?
親疏有別?當然啦,愈親疏的關係,在搜集資訊及履行合同的成本,相對較低。但亦正因如此,取消不合效益的合同,亦相對較難。
有多少企業因親友幫助而起家,卻因用人唯親而衰落?找出平衡點,是不容易的。
中國人的『關係』,是把親疏有別的經濟效益極大化。奇怪的是,美國人也有這樣的事,卻要用『關係』的拼音guanxi來表達。
那麼,怎樣可把『親疏有別』量化?一般而言,兩人愈疏遠,則量化後的距離愈大。
最簡單的,是以互相認識為基礎。若甲與乙互相認識,他倆的距離為1;若甲與乙不相識,但兩人同時認識丙,則甲與乙的距離為2;若甲認識丙,丙認識丁,丁認識乙,則甲與乙的距離為3;如此類推。社會學家Stanley Milgram進行實驗,發覺最遠的距離不超過6。這是個很有趣的人際關係遊戲:隨便找兩個人,看看他們的距離為何?
當然,以上的距離是非常粗糙。同是朋友,點頭朋友或同窗密友自是大不相同。因此要定義新的距離,即以兩人生活圈子多少重疊作計算。若考慮的不是人與人之間的關係,而是網址與網址之間的關係,得到的是以超連結計算的排行傍,當中最有名的要算Google的PageRank。
數據挖掘(Data mining)就是嘗試把不同資料的潛在關係找出來。利用數據挖掘來對人作出分析,是現代社會學研究的一個方向。有報導指美國國防部有收集國民的通訊摸式是以分析,希望找出恐佈分子的溝通模式。成功與否,不曉得,只覺有點《一九八四》味道。
有時候,我們會希望找出兩人某方面的親疏關係。若把之前簡單距離的計算,由相互認識改為有共同文章發表,則可表示二人的學術距離:Erdős number就是數學研究員與多產數學家Paul Erdős的學術距離。
在現實中,互不認識的人可能比互相仇視的人更加親近。又或者親近的感覺並不是雙向的,就如暗戀。若考慮這些,便可能得出更複雜但更準確反映親疏的距離。
有多少企業因親友幫助而起家,卻因用人唯親而衰落?找出平衡點,是不容易的。
中國人的『關係』,是把親疏有別的經濟效益極大化。奇怪的是,美國人也有這樣的事,卻要用『關係』的拼音guanxi來表達。
那麼,怎樣可把『親疏有別』量化?一般而言,兩人愈疏遠,則量化後的距離愈大。
最簡單的,是以互相認識為基礎。若甲與乙互相認識,他倆的距離為1;若甲與乙不相識,但兩人同時認識丙,則甲與乙的距離為2;若甲認識丙,丙認識丁,丁認識乙,則甲與乙的距離為3;如此類推。社會學家Stanley Milgram進行實驗,發覺最遠的距離不超過6。這是個很有趣的人際關係遊戲:隨便找兩個人,看看他們的距離為何?
當然,以上的距離是非常粗糙。同是朋友,點頭朋友或同窗密友自是大不相同。因此要定義新的距離,即以兩人生活圈子多少重疊作計算。若考慮的不是人與人之間的關係,而是網址與網址之間的關係,得到的是以超連結計算的排行傍,當中最有名的要算Google的PageRank。
數據挖掘(Data mining)就是嘗試把不同資料的潛在關係找出來。利用數據挖掘來對人作出分析,是現代社會學研究的一個方向。有報導指美國國防部有收集國民的通訊摸式是以分析,希望找出恐佈分子的溝通模式。成功與否,不曉得,只覺有點《一九八四》味道。
有時候,我們會希望找出兩人某方面的親疏關係。若把之前簡單距離的計算,由相互認識改為有共同文章發表,則可表示二人的學術距離:Erdős number就是數學研究員與多產數學家Paul Erdős的學術距離。
在現實中,互不認識的人可能比互相仇視的人更加親近。又或者親近的感覺並不是雙向的,就如暗戀。若考慮這些,便可能得出更複雜但更準確反映親疏的距離。
Wednesday, May 24, 2006
丹布朗福音
一日丹布朗在家中沈思。突然,電腦顯示器閉出一道耀眼光芒,而擴音器傳出一把雄渾聲音:『丹布朗,丹布朗,聽我說話!』
丹布朗嚇了一跳,問:『誰在叫喚我?』
『我是抺大利瑪利亞的天主,主業會的天主,達文西的天主,騎士團的天主!』
『我的主啊!您要我幹甚麼?』
『我要你把所有的傳說,包括抺大利的瑪利亞與耶穌結婚生子,主業會的謠言,達文西是郇山隠修會成員,騎士團發現耶穌後裔,等等,寫成一部小說!』
『我的主啊!為甚麼?難道這些都是真的?』
『丹布朗,你先答我,你做得到嗎?』
『我的主啊!我可以加上尋寶、暗殺、陰謀、愛情,寫成一部小說。但情節是頗為老套的。』
『老套沒問題,你的小說將會成為震撼!』
『我的主啊!這樣我將受到教會攻擊,那我會得到甚麼?』
『你會如猶大一樣,受千萬基督徒咒罵!但你會名成利就,影嚮力遍佈全球!』
『我的主啊!我願意為您服務!』
『丹布朗,我的忠僕,你還有甚麼問題?』
『我的主啊!為甚麼要寫?難道這些都是真的?』
『真與假沒關係,我要看看信徒的信德,看他們是否因小說動搖,看他們是否因小說大驚小怪!』
『我的主啊!我明白了!我這就去寫。』
『丹布朗,我的忠僕,我祝福你。』
原來這就是《達文西密碼》的因由,阿彌陀佛!
丹布朗嚇了一跳,問:『誰在叫喚我?』
『我是抺大利瑪利亞的天主,主業會的天主,達文西的天主,騎士團的天主!』
『我的主啊!您要我幹甚麼?』
『我要你把所有的傳說,包括抺大利的瑪利亞與耶穌結婚生子,主業會的謠言,達文西是郇山隠修會成員,騎士團發現耶穌後裔,等等,寫成一部小說!』
『我的主啊!為甚麼?難道這些都是真的?』
『丹布朗,你先答我,你做得到嗎?』
『我的主啊!我可以加上尋寶、暗殺、陰謀、愛情,寫成一部小說。但情節是頗為老套的。』
『老套沒問題,你的小說將會成為震撼!』
『我的主啊!這樣我將受到教會攻擊,那我會得到甚麼?』
『你會如猶大一樣,受千萬基督徒咒罵!但你會名成利就,影嚮力遍佈全球!』
『我的主啊!我願意為您服務!』
『丹布朗,我的忠僕,你還有甚麼問題?』
『我的主啊!為甚麼要寫?難道這些都是真的?』
『真與假沒關係,我要看看信徒的信德,看他們是否因小說動搖,看他們是否因小說大驚小怪!』
『我的主啊!我明白了!我這就去寫。』
『丹布朗,我的忠僕,我祝福你。』
原來這就是《達文西密碼》的因由,阿彌陀佛!
Tuesday, May 23, 2006
外判的原罪
兩個菜檔,產品一樣,但價錢不同。我們自然會購買較便宜的。
兩間公司,服務一樣,但收費不同。我們自然會幫趁較便宜的。
兩位工人,質素一樣,但薪金不同。我們自然會僱用較便宜的。
有甚麼問題?
轉過方式:
我們本來已採納一個菜檔,一間公司,一位工人。
忽然有新菜檔,產品一樣,但價錢較低。我們應否轉換菜檔?
忽然有新公司,服務一樣,但收費較低。我們應否轉換公司?
忽然有新工人,質素一樣,但薪金較低。我們應否轉換工人?
若只談經濟,一切好辦(註1)。但,我們對原有的菜檔,公司,工人,有否道義上的責任?
不過甚麼是道義?
有說,美國商人把工序外判給中國,而不留給美國人,是不道德的;而然,把工序外判給數千個中國的貧窮工人,而不是數百個美國工人,不是更加的功德無量嗎?
同理,把香港的職位,給予同是中國人的大陸同胞,為甚麼是沒道義的呢?
說到底,就是『親疏有别』,把自家(包括舊伙伴)的工作外判給他人,就是外判的原罪!
註1:所謂經濟,並不是只看賬面,還要考慮其他可能情況。例如:一、外判後水準下降,短期賬面之得不及長期口啤之失;二、部分工作外判,弄至人心惶惶,反而影嚮生產力。做管理,可不是容易的事啊!
兩間公司,服務一樣,但收費不同。我們自然會幫趁較便宜的。
兩位工人,質素一樣,但薪金不同。我們自然會僱用較便宜的。
有甚麼問題?
轉過方式:
我們本來已採納一個菜檔,一間公司,一位工人。
忽然有新菜檔,產品一樣,但價錢較低。我們應否轉換菜檔?
忽然有新公司,服務一樣,但收費較低。我們應否轉換公司?
忽然有新工人,質素一樣,但薪金較低。我們應否轉換工人?
若只談經濟,一切好辦(註1)。但,我們對原有的菜檔,公司,工人,有否道義上的責任?
不過甚麼是道義?
有說,美國商人把工序外判給中國,而不留給美國人,是不道德的;而然,把工序外判給數千個中國的貧窮工人,而不是數百個美國工人,不是更加的功德無量嗎?
同理,把香港的職位,給予同是中國人的大陸同胞,為甚麼是沒道義的呢?
說到底,就是『親疏有别』,把自家(包括舊伙伴)的工作外判給他人,就是外判的原罪!
註1:所謂經濟,並不是只看賬面,還要考慮其他可能情況。例如:一、外判後水準下降,短期賬面之得不及長期口啤之失;二、部分工作外判,弄至人心惶惶,反而影嚮生產力。做管理,可不是容易的事啊!
Monday, May 22, 2006
策略的作用
今天聽過諾貝爾得奬人Robert J.Aumann的演說,題目為『戰爭與和平』。說的是,短期的合理行為,長期未必是最好。他用的是以下例子:
驟眼看來,若甲貪婪而乙選擇容忍,便是一個平衡。因為沒有一人單獨改變會有更好結果。但如果情況是不斷出現,乙可以用兩敗俱傷的策略來迫使甲公平行事。
且容我用出名的囚犯困境(Prisoner's Dilemma)也來說一說:
若一人戰爭而一人忍耐,發動戰爭者便會得到最大利益,結果是兩人都選擇戰爭,得出最壞結果!但如果情況是不斷出現,一次突襲的甜頭會被將來的戰爭抵消,所以較好的策略是不作發動戰爭者!
阿聯酋的外交官,向猶太裔的講者問及以巴沖突時,得到的答案是:以色列國內的Please Now行動,用意需好,但欲速不達。我想他的意思是,既得利益者的反彈,和得寸進尺的對手,把這個意願扺消了。冀求立即和平並不是正確的策略。
同日另一位講者,也是諾貝爾得奬人Robert A.Mundell,亦說:中國沒有以零通脹作目標,反而平衡了通脹。若以零通脹作目標,令匯率波動太大,反而不利平穩物價。
或者,現在香港的民主黨人,以立即民主為目標,反而令中共有戒心。波闌的團結工會,是多少年的等待,終於成功了。不是說香港也要這麼久才有民主,但民主派人士要有個清淅可行的策略。
同理,加拿大的種族歧視,基本上壓下去了。反歧視立法是有一定作用,但種族主義者可以有不同的方法繞過這條法例。最有效的策略卻是吸納各地的移民,成為不可忽視的經濟和政治力量,令種族主義者為着自身利益也學會包容不同種族。
曾經有台灣人說:台獨是手段。目的是讓中共不敢胡來,兼送來一點甜頭。事實上急獨和急統都會適得其反。兩岸各自放棄急獨及急統,令民間往來帶來小陽春。將來,是那一個的策略較高明,是漸進式台獨,或漸進式統一?
最低公資是不可取的--實施結果是商界及工人兩敗俱傷--但以此作為逼迫商界的手段,卻也管用。從前,商界只懂用工運分子不理解的經濟理論抗辨;但自從多了支持最低工資的議員,商界開始提出「企業責任」或「公司助養」,以回應由低下層來的壓力。不過,這些策略遠遠不能抗衡這股壓力!
唉,天佑香港經濟!
| 乙:忍耐 | 乙:鬥爭 | |
| 甲:貪婪 | 20,0 | -1,-1 |
| 甲:公平 | 10,10 | -1,-1 |
驟眼看來,若甲貪婪而乙選擇容忍,便是一個平衡。因為沒有一人單獨改變會有更好結果。但如果情況是不斷出現,乙可以用兩敗俱傷的策略來迫使甲公平行事。
且容我用出名的囚犯困境(Prisoner's Dilemma)也來說一說:
| 乙:忍耐 | 乙:戰爭 | |
| 甲:忍耐 | 10,10 | 0,20 |
| 甲:戰爭 | 20,0 | -1,-1 |
若一人戰爭而一人忍耐,發動戰爭者便會得到最大利益,結果是兩人都選擇戰爭,得出最壞結果!但如果情況是不斷出現,一次突襲的甜頭會被將來的戰爭抵消,所以較好的策略是不作發動戰爭者!
阿聯酋的外交官,向猶太裔的講者問及以巴沖突時,得到的答案是:以色列國內的Please Now行動,用意需好,但欲速不達。我想他的意思是,既得利益者的反彈,和得寸進尺的對手,把這個意願扺消了。冀求立即和平並不是正確的策略。
同日另一位講者,也是諾貝爾得奬人Robert A.Mundell,亦說:中國沒有以零通脹作目標,反而平衡了通脹。若以零通脹作目標,令匯率波動太大,反而不利平穩物價。
或者,現在香港的民主黨人,以立即民主為目標,反而令中共有戒心。波闌的團結工會,是多少年的等待,終於成功了。不是說香港也要這麼久才有民主,但民主派人士要有個清淅可行的策略。
同理,加拿大的種族歧視,基本上壓下去了。反歧視立法是有一定作用,但種族主義者可以有不同的方法繞過這條法例。最有效的策略卻是吸納各地的移民,成為不可忽視的經濟和政治力量,令種族主義者為着自身利益也學會包容不同種族。
曾經有台灣人說:台獨是手段。目的是讓中共不敢胡來,兼送來一點甜頭。事實上急獨和急統都會適得其反。兩岸各自放棄急獨及急統,令民間往來帶來小陽春。將來,是那一個的策略較高明,是漸進式台獨,或漸進式統一?
最低公資是不可取的--實施結果是商界及工人兩敗俱傷--但以此作為逼迫商界的手段,卻也管用。從前,商界只懂用工運分子不理解的經濟理論抗辨;但自從多了支持最低工資的議員,商界開始提出「企業責任」或「公司助養」,以回應由低下層來的壓力。不過,這些策略遠遠不能抗衡這股壓力!
唉,天佑香港經濟!
Friday, May 19, 2006
螞蟻
螞蟻可以說是全球最先建設大都會的生物。由六千萬年前起便開始成立以女王為中心的國度,國民動軌逾百萬。
有些螞蟻懂得剪裁,用樹枼造穚造屋。有些螞蟻懂得耕種,種的是箘,可供食用。
有些螞蟻懂飛,有些螞蟻懂游。有些螞蟻只懂吃,成為其他螞蟻的奶媽。
螞蟻可以在任何環境,包括在水中或沙中,建立王國。螞蟻可以在短時間內改變一個地區的面貎,倚仗的是龐大的動員力。工具不是只鋒利的咀,也可以是有毒的化學品。
螞蟻社會是階級分明的,一出生便決定了未來地位。所有子民都聽聽話話,不存在背叛。
有些國度可以聯盟結成一個超級王朝。有些國度可以有超過一個女王。
螞蟻之間的戰爭可以非常慘烈。多數螞蟻會戰死,
有些螞蟻懂得詐死,躱避敵蟻。但也有的會成為俘擄,成為其他王國的工蟻。有些王國沒有俘擄是不能運作的。
愈說愈像人類社會。最相像的,是人間帝國與螞蟻王國的國民都喚作『蟻民』!
有些螞蟻懂得剪裁,用樹枼造穚造屋。有些螞蟻懂得耕種,種的是箘,可供食用。
有些螞蟻懂飛,有些螞蟻懂游。有些螞蟻只懂吃,成為其他螞蟻的奶媽。
螞蟻可以在任何環境,包括在水中或沙中,建立王國。螞蟻可以在短時間內改變一個地區的面貎,倚仗的是龐大的動員力。工具不是只鋒利的咀,也可以是有毒的化學品。
螞蟻社會是階級分明的,一出生便決定了未來地位。所有子民都聽聽話話,不存在背叛。
有些國度可以聯盟結成一個超級王朝。有些國度可以有超過一個女王。
螞蟻之間的戰爭可以非常慘烈。多數螞蟻會戰死,
有些螞蟻懂得詐死,躱避敵蟻。但也有的會成為俘擄,成為其他王國的工蟻。有些王國沒有俘擄是不能運作的。
愈說愈像人類社會。最相像的,是人間帝國與螞蟻王國的國民都喚作『蟻民』!
Friday, May 12, 2006
女人的歷史
猶太神話中第一對男女是亞當與夏娃。生物學中也有亞當與夏娃,被認為是所有人的祖先,但他倆卻不是配偶。
男人的Y染色體,是由父親傳下來的,從這條路住回走,會追溯到一個非洲男人,被稱為Y染色體亞當(Y-chromosomal Adam),生於6萬年前。女人的染色體,可由父或母傳下來,但細胞中的線粒體,多是從母親而來,從這條路住回走,會追溯到一個非洲女人,被稱為線粒體夏娃(Mitochondrial Eve),生於約十五萬年前。用現代標準來看,Y染色體亞當無可置疑是真正的人,但線粒體夏娃還可能只是個野人!
憑着線粒體的研究,可以得出一部生物學上女人的歷史,而這部女人歷史,是不是從線粒體夏娃開始的?
現存最古老的女性骸骨,是4百萬年前的lucy,不過她不是現代人的祖先,而且基本不是用兩條腿走路,近猿多於人。第一個女人,不知道是在那時出現,不過肯定不是線粒體夏娃。我們只知道夏娃同期女性的後代基本上都被淘汰了。既然如此,我們不妨讓這部歷史由夏娃開始。
據估計,夏娃時期,人類基本上是母系社會。隨着時間演進,泰半社會都轉成父系,但仍然有一些保留着母系社會特性,例如摩梭人。歷史上是否存在女人有絕對權力的國度?只有一個,就是傳說中生活於亞細亞的亞馬遜族,所有女人都是饒勇善戰的。
接下來的女人歷史,看來和男人歷史沒分別。事實上,也真的沒大分別。因為男人可以遺傳所有女人的基因。嘿,我從來都在說生物學上的歷史,不是說社會的歷史。
想測試自己基因,幫忙撰寫人類基因史,同時知道自己的老祖宗從何而來?可進入Genographic Project的網址
https://www3.nationalgeographic.com/genographic/index.html
不過要給錢的。
男人的Y染色體,是由父親傳下來的,從這條路住回走,會追溯到一個非洲男人,被稱為Y染色體亞當(Y-chromosomal Adam),生於6萬年前。女人的染色體,可由父或母傳下來,但細胞中的線粒體,多是從母親而來,從這條路住回走,會追溯到一個非洲女人,被稱為線粒體夏娃(Mitochondrial Eve),生於約十五萬年前。用現代標準來看,Y染色體亞當無可置疑是真正的人,但線粒體夏娃還可能只是個野人!
憑着線粒體的研究,可以得出一部生物學上女人的歷史,而這部女人歷史,是不是從線粒體夏娃開始的?
現存最古老的女性骸骨,是4百萬年前的lucy,不過她不是現代人的祖先,而且基本不是用兩條腿走路,近猿多於人。第一個女人,不知道是在那時出現,不過肯定不是線粒體夏娃。我們只知道夏娃同期女性的後代基本上都被淘汰了。既然如此,我們不妨讓這部歷史由夏娃開始。
據估計,夏娃時期,人類基本上是母系社會。隨着時間演進,泰半社會都轉成父系,但仍然有一些保留着母系社會特性,例如摩梭人。歷史上是否存在女人有絕對權力的國度?只有一個,就是傳說中生活於亞細亞的亞馬遜族,所有女人都是饒勇善戰的。
接下來的女人歷史,看來和男人歷史沒分別。事實上,也真的沒大分別。因為男人可以遺傳所有女人的基因。嘿,我從來都在說生物學上的歷史,不是說社會的歷史。
想測試自己基因,幫忙撰寫人類基因史,同時知道自己的老祖宗從何而來?可進入Genographic Project的網址
https://www3.nationalgeographic.com/genographic/index.html
不過要給錢的。
Tuesday, May 09, 2006
男人的歷史
有個笑話,說英文history是“his story”即“男人的歷史”,是有性別歧視的字。不過當真的,大部分歷史都是父權中心,這解釋似乎倒也沒錯。
第一個男人是誰?根據基督教的教義,這人的名字叫亞當。生物學家也相信現在所有男人,都有Y染色體只會由父傳子,從Y染色體的自然突變頻率,可以得出一部生理學上的男人歷史。這正是《國家地理雜誌》與IBM合作的Genographic Project的一部分。
那這部歷史是如何開始的呢?很多宗教或民間傳說,都有第一個男人。最有名的,是基督教的阿當,他和第一個女人夏娃有兩個兒子--大兒子後來殺死了小兒子,被放逐,和不知從何而來的女人結婚。
進化論家怎說?
第一個『似人』的生物,是生活在600萬年前的「乍得人猿」(Sahelanthropus tchadensis),這當然不是人。現代人類,即「晚期智人」(Homo Sapiens Sapiens),估計在20萬年前出現。
大約5萬年前,一種有巧手工藝的文明出現,與此同期一種新的Y染色體變異產生。Genographic Project的主持人Spencer Wells認為兩者是有關係的。這個新的非洲男人,是所有男人的祖先,亦被稱為亞當(Y-chromosomal Adam)。這個非洲男人及他的子裔,憑着過人的才智,終於把其他的人種淘汰。這部男人歷史就是如此開始。
四海之內,皆兄弟也,最多只是隔了二千世代罷!
我們基本上已大約知道人類的遷移路徑,例如澳洲土箸是由印度大陸過去,第一代歐洲人是由中東過去等等。我們知道大約有1600萬人是成吉思汗皇族的後人。有興趣的,可閱讀Spencer Wells的《The Journey of Man: A Genetic Odyssey》。
Genographic Project,希望收集更多人的遺傳因子,從而為很多歷史或傳說的秘密(究竟腓利基人-第一套字母的創始者-的後人在那裡?哪些人是猶太失落的分支?),給出一點暗示。我在釋目以待!
第一個男人是誰?根據基督教的教義,這人的名字叫亞當。生物學家也相信現在所有男人,都有Y染色體只會由父傳子,從Y染色體的自然突變頻率,可以得出一部生理學上的男人歷史。這正是《國家地理雜誌》與IBM合作的Genographic Project的一部分。
那這部歷史是如何開始的呢?很多宗教或民間傳說,都有第一個男人。最有名的,是基督教的阿當,他和第一個女人夏娃有兩個兒子--大兒子後來殺死了小兒子,被放逐,和不知從何而來的女人結婚。
進化論家怎說?
第一個『似人』的生物,是生活在600萬年前的「乍得人猿」(Sahelanthropus tchadensis),這當然不是人。現代人類,即「晚期智人」(Homo Sapiens Sapiens),估計在20萬年前出現。
大約5萬年前,一種有巧手工藝的文明出現,與此同期一種新的Y染色體變異產生。Genographic Project的主持人Spencer Wells認為兩者是有關係的。這個新的非洲男人,是所有男人的祖先,亦被稱為亞當(Y-chromosomal Adam)。這個非洲男人及他的子裔,憑着過人的才智,終於把其他的人種淘汰。這部男人歷史就是如此開始。
四海之內,皆兄弟也,最多只是隔了二千世代罷!
我們基本上已大約知道人類的遷移路徑,例如澳洲土箸是由印度大陸過去,第一代歐洲人是由中東過去等等。我們知道大約有1600萬人是成吉思汗皇族的後人。有興趣的,可閱讀Spencer Wells的《The Journey of Man: A Genetic Odyssey》。
Genographic Project,希望收集更多人的遺傳因子,從而為很多歷史或傳說的秘密(究竟腓利基人-第一套字母的創始者-的後人在那裡?哪些人是猶太失落的分支?),給出一點暗示。我在釋目以待!
索馬里的電訊業
去年十一月,BBC報導索馬里蓬勃的電訊業(http://news.bbc.co.uk/2/hi/africa/4020259.stm),顯示了在無政府的狀態下,自由經濟的威力。
沒有政府,不用交稅,不用牌照費,也沒有籠斷的國有電訊公司。結果是索馬里幾乎是全非洲電訊收費最便宜的地方。
公共交通設施在戰爭中被摧毁,但私人的港口及機場,令設備輸入仍而暢通。
銀行制度崩潰,但傳統的宗族力量,使交易可如常運行。
令人煩惱的保安問題,只是偶然的鼠竊狗偷,大軍閥不希望電話不通,倒與電訊公司互不干泄。
但有利,必有弊。被視為既有利益者的電訊老闆,也希望有政府,即使要交稅。為甚麼呢?
建全的銀行制度,成本效益及方便遠勝傳統的宗族系統。猶以向外國購買器材為甚。
破落的教育制度,要送職員到海外受訓,增加成本。
個人安全沒保障,如果可以量化的話,無政府狀態下的保安要極大成本。
還有一樣是報導沒有提及的,是在無政府狀態下,白紙黑字的法律被潛規則代替。掌握潛規則比掌握法律更難,這表示需要更大的無形成本!
所以政府的一個責任,是要減低交易成本,不管有形或無形的。
索馬里的不幸的,它還不斷受戰火摧殘;但不幸中之大幸,相對完備的電訊業,及海外的大量僑胞(近乎總人口的二成),令這國度不致成了讓人遺忘、沒有希望的國家。
據報導,那裡的電訊公司還打算引入3G。不知怎的,聽上去好像有點諷刺。
沒有政府,不用交稅,不用牌照費,也沒有籠斷的國有電訊公司。結果是索馬里幾乎是全非洲電訊收費最便宜的地方。
公共交通設施在戰爭中被摧毁,但私人的港口及機場,令設備輸入仍而暢通。
銀行制度崩潰,但傳統的宗族力量,使交易可如常運行。
令人煩惱的保安問題,只是偶然的鼠竊狗偷,大軍閥不希望電話不通,倒與電訊公司互不干泄。
但有利,必有弊。被視為既有利益者的電訊老闆,也希望有政府,即使要交稅。為甚麼呢?
建全的銀行制度,成本效益及方便遠勝傳統的宗族系統。猶以向外國購買器材為甚。
破落的教育制度,要送職員到海外受訓,增加成本。
個人安全沒保障,如果可以量化的話,無政府狀態下的保安要極大成本。
還有一樣是報導沒有提及的,是在無政府狀態下,白紙黑字的法律被潛規則代替。掌握潛規則比掌握法律更難,這表示需要更大的無形成本!
所以政府的一個責任,是要減低交易成本,不管有形或無形的。
索馬里的不幸的,它還不斷受戰火摧殘;但不幸中之大幸,相對完備的電訊業,及海外的大量僑胞(近乎總人口的二成),令這國度不致成了讓人遺忘、沒有希望的國家。
據報導,那裡的電訊公司還打算引入3G。不知怎的,聽上去好像有點諷刺。
Sunday, May 07, 2006
為『弱肉强食』平反
『弱肉强食』是甚麼?正確一點,是『弱者淘汰,强者留下』。
就如獅子吃岭羊:最弱的獅子捉不到獵物,因而餓死;最强的獅子捉到獵物,可以生存;最弱的岭羊逃不掉,因而被殺;最强的岭羊走掉了,可以生存。
就如超市與小商戶爭市場:不能因時制宜的小商戶,被受淘汰;有實力的小商戶(如我樓下街角的菜擋老闆),仍能笑傲江湖;經營不善的超市(如當年的華潤超市),逃不過結業;經營得法的超市,當然利潤豐厚。
就如大國和小國之爭:强大的大國吞併弱小的小國,是司空見慣;但强大的小國吞併弱小的大國,其實也不罕見,有名的是馬其頓統治希臘,或滿洲吞噬大明。
哪麼,『弱肉强食』有何不對?
答案:『弱肉强食』沒有甚麼不對,但也沒有甚麼對。『弱肉强食』只是一種現象,就如日出日落,沒有對或不對。
不知從甚麼時候開始,『弱肉强食』被看作是生物界的規則。但生物界其實只有一種規則:求存!『弱肉强食』是生物為求生所引致的現象。
除了『弱肉强食』外,還有很多生物界現象,包括『共生』、『分工』、『亂倫』、『弒夫』、『收飬』、『結盟』、『戰爭』、『偷盜』。
雖然人的社會行為或者可以用生物學解釋,但一種行為在生物界出現並不能成為被人類社會接受的籍口。
當然囉,一種行為並不在生物界出現亦不能成為不被人類社會接受的籍口。天曉得這行為是否只是未被發現而已!
我以為,『弱肉强食』對與不對,應是以其目的作準。其實,很多時候,反對『弱肉强食』的人,只是反對『利益極大化』而已--證明是,他們往往反對大企業吞食小企業,但對小企業間的弱肉强食,卻視而不見!
就如獅子吃岭羊:最弱的獅子捉不到獵物,因而餓死;最强的獅子捉到獵物,可以生存;最弱的岭羊逃不掉,因而被殺;最强的岭羊走掉了,可以生存。
就如超市與小商戶爭市場:不能因時制宜的小商戶,被受淘汰;有實力的小商戶(如我樓下街角的菜擋老闆),仍能笑傲江湖;經營不善的超市(如當年的華潤超市),逃不過結業;經營得法的超市,當然利潤豐厚。
就如大國和小國之爭:强大的大國吞併弱小的小國,是司空見慣;但强大的小國吞併弱小的大國,其實也不罕見,有名的是馬其頓統治希臘,或滿洲吞噬大明。
哪麼,『弱肉强食』有何不對?
答案:『弱肉强食』沒有甚麼不對,但也沒有甚麼對。『弱肉强食』只是一種現象,就如日出日落,沒有對或不對。
不知從甚麼時候開始,『弱肉强食』被看作是生物界的規則。但生物界其實只有一種規則:求存!『弱肉强食』是生物為求生所引致的現象。
除了『弱肉强食』外,還有很多生物界現象,包括『共生』、『分工』、『亂倫』、『弒夫』、『收飬』、『結盟』、『戰爭』、『偷盜』。
雖然人的社會行為或者可以用生物學解釋,但一種行為在生物界出現並不能成為被人類社會接受的籍口。
當然囉,一種行為並不在生物界出現亦不能成為不被人類社會接受的籍口。天曉得這行為是否只是未被發現而已!
我以為,『弱肉强食』對與不對,應是以其目的作準。其實,很多時候,反對『弱肉强食』的人,只是反對『利益極大化』而已--證明是,他們往往反對大企業吞食小企業,但對小企業間的弱肉强食,卻視而不見!
從卵子融合到純女性世界
一個卵子有包含x染色體的23條染色體。兩個卵子給合為一,就有包括xx的23對染色體,便成了一個完整的女性細胞。
當然現實並非如此簡單,但在2004年日本科學家成功把兩個老鼠卵子融合成一個細胞並製造出沒父親的老鼠後,似乎向『理想』邁進一步。(註1)
若卵子融合真的成功,女同性戀人可以有生理上兩人共同擁有的下一代,而且只會是女兒。現在的女同性戀社區仍雖要以「移民」來維持,將來可發展成一個自給自足的社區。
即使沒有卵子融合,複製人技術也可以帶來純女性社會,但由基因混雜而帶來的潛在好處卻會失去。
有人認為純女性世界將來一定會來臨。皆因有證據說y染色體在過去千萬年在不斷縮短,若情況持續,終有一天y染色體(即男性)會消失。
那麼,這個純女性世界,和現在有何分别?分別應該不大,甚至性別歧視依然存在--雖然生物學定義的男性不復見,但從心理行為定義的男性仍然存在。
在《星空奇遇記續集》中,有一集談及一個單性世界。若然有些成員出現男性或女性傾向,便被視為精神異常,要接受治療。
在《龍球》中,撒亞人也是個單性世界。但因為所有撒亞人是由單一『父親』所出,社會結構近乎螞蟻,對『父親』絕對忠心。
亦曾有一套電視片(忘記了名字),說未來是個純女性世界,卻是倚靠上古冷藏的精子繁殖。即使成功誔下男孩,也會夭折。奇怪的是,所有女性都仍以現代的女性行為所標準!
各位朋友,你心目中的單性世界是怎樣的呢?(註2)
(註1)在google搜尋"fatherless mouse"會有更多資訊。
(註2)說的是沒有第二性的世界,並不是在兩性世界中的單性社區!
當然現實並非如此簡單,但在2004年日本科學家成功把兩個老鼠卵子融合成一個細胞並製造出沒父親的老鼠後,似乎向『理想』邁進一步。(註1)
若卵子融合真的成功,女同性戀人可以有生理上兩人共同擁有的下一代,而且只會是女兒。現在的女同性戀社區仍雖要以「移民」來維持,將來可發展成一個自給自足的社區。
即使沒有卵子融合,複製人技術也可以帶來純女性社會,但由基因混雜而帶來的潛在好處卻會失去。
有人認為純女性世界將來一定會來臨。皆因有證據說y染色體在過去千萬年在不斷縮短,若情況持續,終有一天y染色體(即男性)會消失。
那麼,這個純女性世界,和現在有何分别?分別應該不大,甚至性別歧視依然存在--雖然生物學定義的男性不復見,但從心理行為定義的男性仍然存在。
在《星空奇遇記續集》中,有一集談及一個單性世界。若然有些成員出現男性或女性傾向,便被視為精神異常,要接受治療。
在《龍球》中,撒亞人也是個單性世界。但因為所有撒亞人是由單一『父親』所出,社會結構近乎螞蟻,對『父親』絕對忠心。
亦曾有一套電視片(忘記了名字),說未來是個純女性世界,卻是倚靠上古冷藏的精子繁殖。即使成功誔下男孩,也會夭折。奇怪的是,所有女性都仍以現代的女性行為所標準!
各位朋友,你心目中的單性世界是怎樣的呢?(註2)
(註1)在google搜尋"fatherless mouse"會有更多資訊。
(註2)說的是沒有第二性的世界,並不是在兩性世界中的單性社區!
Sunday, April 30, 2006
難與深
朋友說我近期寫的太難太深,這可是我的老毛病。
不過,這也是數學的問題。
我寫的,只算是現代數學基礎,但基礎不等於容易。
情形等於:化學的基礎在原子,物理的基礎在能量,經濟的基礎在交易資本。
科學之所以難,因為學習的起點是在中間出發,而不是由基礎結構開始。原因是基礎構不能通過感觀接觸了解。一個學術的基礎結構並不是該學術的基礎學問!
一個永恆的教育難題,是在甚麼時候開始教導教基礎結構。
不過,這也是數學的問題。
我寫的,只算是現代數學基礎,但基礎不等於容易。
情形等於:化學的基礎在原子,物理的基礎在能量,經濟的基礎在交易資本。
科學之所以難,因為學習的起點是在中間出發,而不是由基礎結構開始。原因是基礎構不能通過感觀接觸了解。一個學術的基礎結構並不是該學術的基礎學問!
一個永恆的教育難題,是在甚麼時候開始教導教基礎結構。
Friday, April 21, 2006
數字是個遊戲
『數字是個遊戲。』誰人會說這樣的話?
一個見慣風浪,歷盡起跌的股壇老手?
一個不負責任,專個假賬的會計敗類?
一個腰纏萬貫,勝負等閒的商界巨賈?
一個強作瀟洒,生活平實的過氣富翁?
一個活動教學,負責數學的小學老師?
若通通不是,可能這人是個研究組合遊戲理論的數學家。
組合遊戲理論是研究純技術的博奕遊戲,例如圍棋、象棋、拿火柴遊戲。麻將、飛行棋、天九等不在其研究範圍;橋牌、鋤大弟、十三張等也不在其研究範圍--因要猜對方手中的牌,也有運氣成分。數學家主要是研究二人博奕。
Ernst Zermelo (1871-1953) 率先證明所有二人博奕都應是早知結果的!要麼是先行者有必勝(應是不敗)策略,要麼是後行者有必勝方法,這當然視乎是何類遊戲。(見〔1〕)

約翰.康威(John H. Conway)提出了個有趣的定義:一個 (L|R) 是個遊戲如果 L 及 R 也是個遊戲--這定義可用於尋找必勝策略。他與兩位重量級人物在著作《穩操勝券(上下冊)》(Winning Ways for your Mathematical Plays)有講述這定義的應用,這本書在一般書局有售。
若然限制 L < R(何謂大小,這不贅),就是超實數 surreal numbers,一種包含無限大及無窮小的數字系統!這個慨念是建基於Dedekind cuts,本來用於透過分數定義實數。
所以,『數字是個遊戲。』可是有真正數學意義的啊!
一個見慣風浪,歷盡起跌的股壇老手?
一個不負責任,專個假賬的會計敗類?
一個腰纏萬貫,勝負等閒的商界巨賈?
一個強作瀟洒,生活平實的過氣富翁?
一個活動教學,負責數學的小學老師?
若通通不是,可能這人是個研究組合遊戲理論的數學家。
組合遊戲理論是研究純技術的博奕遊戲,例如圍棋、象棋、拿火柴遊戲。麻將、飛行棋、天九等不在其研究範圍;橋牌、鋤大弟、十三張等也不在其研究範圍--因要猜對方手中的牌,也有運氣成分。數學家主要是研究二人博奕。
Ernst Zermelo (1871-1953) 率先證明所有二人博奕都應是早知結果的!要麼是先行者有必勝(應是不敗)策略,要麼是後行者有必勝方法,這當然視乎是何類遊戲。(見〔1〕)

約翰.康威(John H. Conway)提出了個有趣的定義:一個 (L|R) 是個遊戲如果 L 及 R 也是個遊戲--這定義可用於尋找必勝策略。他與兩位重量級人物在著作《穩操勝券(上下冊)》(Winning Ways for your Mathematical Plays)有講述這定義的應用,這本書在一般書局有售。
若然限制 L < R(何謂大小,這不贅),就是超實數 surreal numbers,一種包含無限大及無窮小的數字系統!這個慨念是建基於Dedekind cuts,本來用於透過分數定義實數。
所以,『數字是個遊戲。』可是有真正數學意義的啊!
Thursday, April 20, 2006
超越現實的數
不懂數學的人, 可能也會接受無限大及無窮小;反而對數學家,接受無限大及無窮小會有邏輯上的問題。
當Abraham Robinson成功創造出包含無限大和無窮小,且邏輯上可行的數字系統,在數學界產生頗大迴響。這系統是 hyperreal numbers。最簡單的解釋,系統內每個數其實是個數列--7 是 (7,7,7,...) 而 -8 是 (-8,-8,...,-8);無限大是不斷增大的數列,如 (1,2,3,4,...) 及 (1,3,5,7,...) 便是兩個無限大;無窮小是愈來愈接近0的數列,如 (1,1/2,1/3,1/4,...) 及 (1,0.1,0.01,0.001,...)便是兩個無窮小。當然還有其他理論上的限制。
稍後, John Horton Conway發明了另一套數字系統,也包含無限大和無窮小,產生的不是迴響,而是震撼!這系統是 surreal numbers。Conway 運用了載得金分割(Dedekind cuts)的意念,成功的把現代數學中多個不同的範疇(實數,序數,組合理論)連繫起來。很難三言兩語說明 Conway 的理論解釋,但可以說的是,他證明了『數字是個遊戲』!事實上,Conway 發展這理論真的是要研究一種遊戲--我國的國技『圍棋』!!!
可能是遺撼,兩者的中文名稱都是超實數。還有另一個超實數 superreal numbers,是 hyperreal numbers 的再擴張。
某程度來說,日常生活中或許不會遇到這些數,超實數可謂名副其實;但從數學上而言,超實數與實數同樣真實。
當Abraham Robinson成功創造出包含無限大和無窮小,且邏輯上可行的數字系統,在數學界產生頗大迴響。這系統是 hyperreal numbers。最簡單的解釋,系統內每個數其實是個數列--7 是 (7,7,7,...) 而 -8 是 (-8,-8,...,-8);無限大是不斷增大的數列,如 (1,2,3,4,...) 及 (1,3,5,7,...) 便是兩個無限大;無窮小是愈來愈接近0的數列,如 (1,1/2,1/3,1/4,...) 及 (1,0.1,0.01,0.001,...)便是兩個無窮小。當然還有其他理論上的限制。
稍後, John Horton Conway發明了另一套數字系統,也包含無限大和無窮小,產生的不是迴響,而是震撼!這系統是 surreal numbers。Conway 運用了載得金分割(Dedekind cuts)的意念,成功的把現代數學中多個不同的範疇(實數,序數,組合理論)連繫起來。很難三言兩語說明 Conway 的理論解釋,但可以說的是,他證明了『數字是個遊戲』!事實上,Conway 發展這理論真的是要研究一種遊戲--我國的國技『圍棋』!!!
可能是遺撼,兩者的中文名稱都是超實數。還有另一個超實數 superreal numbers,是 hyperreal numbers 的再擴張。
某程度來說,日常生活中或許不會遇到這些數,超實數可謂名副其實;但從數學上而言,超實數與實數同樣真實。
Wednesday, April 19, 2006
虛與實,數系的發展
上古時,人只懂1,2,3,...--這是他們的數。
然後,他們需要細分物件,於是出現分數,即兩數之比 a/b--他們認為原先的1,2,3,...才是實在的數,現稱自然數。
然後,有些數量(例如某些長度),是不可以寫成分數--他們(古希臘畢達哥拉斯學派)認為原先的分數才是實在的數,而新發現的數是假的數,傳說中他們甚至殺死Hippasus(第一個發現無理數的人)。分數的希臘文λογος ,意為「成比例的數」(rational number),中文錯譯為有理數,沒理由的數,但這與古希臘人的想法暗合。新發現的數,即「不成比例的數」(irrational number)被譯為無理數。
然後,在尋找多項式 a0+a1x+a2x²+...+anxⁿ=0 的根,不可避免遇到負數的開方--他們認為原先的數(不論有理數或無理數)才實在,是實數,而負數的開方是虛無的數,即虛數。實數與虛數相加,稱為複數。
但後來發現:複數 x+√-1 y 可看作平面上的一點 (x,y),是個二元的數。由此看來,複數非常實在。
數學家開始放開虛實的迷思,得出四元數、八元數、p-進數、超實數、超複數。
但『數』是甚麼?在乎你需要甚麼!
然後,他們需要細分物件,於是出現分數,即兩數之比 a/b--他們認為原先的1,2,3,...才是實在的數,現稱自然數。
然後,有些數量(例如某些長度),是不可以寫成分數--他們(古希臘畢達哥拉斯學派)認為原先的分數才是實在的數,而新發現的數是假的數,傳說中他們甚至殺死Hippasus(第一個發現無理數的人)。分數的希臘文λογος ,意為「成比例的數」(rational number),中文錯譯為有理數,沒理由的數,但這與古希臘人的想法暗合。新發現的數,即「不成比例的數」(irrational number)被譯為無理數。
然後,在尋找多項式 a0+a1x+a2x²+...+anxⁿ=0 的根,不可避免遇到負數的開方--他們認為原先的數(不論有理數或無理數)才實在,是實數,而負數的開方是虛無的數,即虛數。實數與虛數相加,稱為複數。
但後來發現:複數 x+√-1 y 可看作平面上的一點 (x,y),是個二元的數。由此看來,複數非常實在。
數學家開始放開虛實的迷思,得出四元數、八元數、p-進數、超實數、超複數。
但『數』是甚麼?在乎你需要甚麼!
虛(數)與實(數)
以下是兩個常見的數學謎語:
1. 背着喇叭;
2. 大夫診症;
謎底稍後揭曉。
在中學時期,我們知道 ax² +bx+c=0 的兩個解可表達成 (-b ± √ (b² -4ac))/2。
原來 ax³ +bx² +cx+d=0 的三個解也有一般表達式,最簡單的一個是
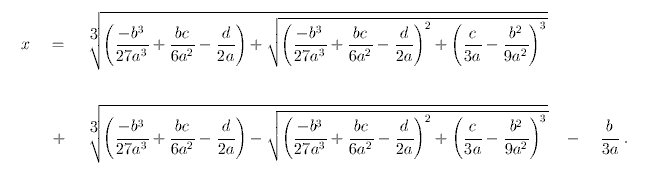
這個解在十六世紀時經已被發現,但卻出現了個問題:考慮 x³ -15x-4=0,它的所有答案是 -3.73, -0.26, 4。若用以上的算式,卻出現不知所謂的 √-109(用計算機試試,九成會送你一個 Error),這條算式似乎用不着!
數學家的解決方法很簡單,首先讓 √-109 = i √109 (這裡i=√-1),然後把i當作一般數字來計,最後所有i會相互抵消!但如 i √109 般的數,令人感覺虛無飄眇,故稱作『虛數』。
這時,人們倒過來說一般的數字是『實數』,即是實在的數。
但正如自然數並不比其他數自然¹,實數的『實』和虛數的『虛』相差其實不大。若考慮二維平面,實數與虛數只是橫軸與縱軸之分而已!
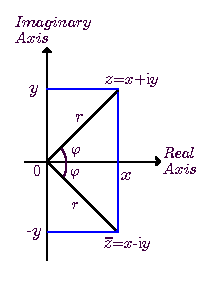 這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
謎語答案:1. 負號;2. 開方。
正數加上負號再開方,便是虛數!
註1:請參看《自然的數?》。
註2:開方只取“正值”,如√4=2但4的平方根是 ±2,這兒 -4 的平方根是 ±2i,2i 的平方根是 ±(1+i),3-4i 的平方根是 ±(2-i)。
1. 背着喇叭;
2. 大夫診症;
謎底稍後揭曉。
在中學時期,我們知道 ax² +bx+c=0 的兩個解可表達成 (-b ± √ (b² -4ac))/2。
原來 ax³ +bx² +cx+d=0 的三個解也有一般表達式,最簡單的一個是
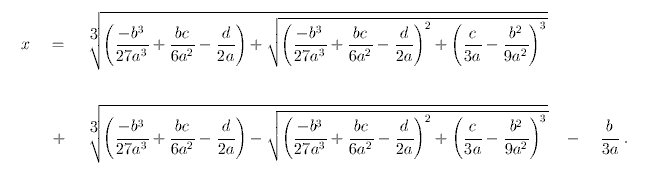
這個解在十六世紀時經已被發現,但卻出現了個問題:考慮 x³ -15x-4=0,它的所有答案是 -3.73, -0.26, 4。若用以上的算式,卻出現不知所謂的 √-109(用計算機試試,九成會送你一個 Error),這條算式似乎用不着!
數學家的解決方法很簡單,首先讓 √-109 = i √109 (這裡i=√-1),然後把i當作一般數字來計,最後所有i會相互抵消!但如 i √109 般的數,令人感覺虛無飄眇,故稱作『虛數』。
這時,人們倒過來說一般的數字是『實數』,即是實在的數。
但正如自然數並不比其他數自然¹,實數的『實』和虛數的『虛』相差其實不大。若考慮二維平面,實數與虛數只是橫軸與縱軸之分而已!
 這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。謎語答案:1. 負號;2. 開方。
正數加上負號再開方,便是虛數!
註1:請參看《自然的數?》。
註2:開方只取“正值”,如√4=2但4的平方根是 ±2,這兒 -4 的平方根是 ±2i,2i 的平方根是 ±(1+i),3-4i 的平方根是 ±(2-i)。
Monday, April 17, 2006
天與地,大與小,冷與熱
『道可道,非常道;名可名,非常名。』--這是《道德經》 的第一句,亦是最耳熟能詳的一句。我想說說:名可名,非常名。
若我們的祖先把「天」喚作「地」,而把「地」喚作「天」,那未現在便會是“地在上,天在下”了。相類的情況是,不同是事物,喚作一樣的名稱,如「天花」是指一種傳染病或是指屋頂底部,所以要清楚名字背後的意義。
原來,這是學生學習數學的一個大障礙!
名稱的改變:-
首先是代數,是以符號代數字,從而達到一般化的運用。卻出現明白3×(4+2)=3×4+3×2,卻不明白 x(y+z)=xy+xz。
然後是最優化,教了學生怎樣求得最大值,他們卻往往未能舉一反三地求出最小值。大與小,很多時只是換個名稱而已!
定義(含義)的不同:-
首先是關係,不同的場合,大小的定義可能完全不同。一般來說,我們會說 4>2>1>-3;但這並非絕對!
在玩橋牌的時候,我們有1>4>2;在玩“鋤大弟”的時候,我們知道 2>1>4。但若我們不提橋牌,不提鋤大弟,而只說 1>4>2 或 2>1>4,學生會頓時不知所措!!!
在物理學中,若以 K 為温度單位,負温度會比正温度為熱。若以>表示比較熱,則有-3>4>2>1!
然後是擴張,隨着認知深化,需要擴張定義符合實況。在初學複數時,學生仍會給舊認知 “沒有「數」的平方是負數” 所跘着,不理解「數」的定義已改變。
在高級代數書中,a1=a=1a並不單是表示數的乘法(a× 1=a=1× a),亦可表示數的加法(a+0=a=0+a),用意是把「乘法」擴張以覆蓋所有性質相近的運算,減省研究的重複性。可想而知,學生多數未能了解。
在中學物理學中,我們是以温度定義冷熱,但大學時,我們以能量流向定義冷熱。
***********************
在文學中,「名」也有難題。在一些文化中,一個人往往有着不同的稱謂,或者一個家族不同人有相同的名稱,令記性不大好的人(如在下)難於閱讀相關傳記或小說!
例如,三國演義中,一人往往有着三個或以上的稱呼,如諸葛亮,字孔明,號臥龍先生;
又如世界首富比爾蓋茨(William Henry Gates III)的父親也是比爾蓋茨(William Henry Gates, Sr.)!
科學與文學中的「名」已這麼難掌握,更何況哲學中的「名」?
若我們的祖先把「天」喚作「地」,而把「地」喚作「天」,那未現在便會是“地在上,天在下”了。相類的情況是,不同是事物,喚作一樣的名稱,如「天花」是指一種傳染病或是指屋頂底部,所以要清楚名字背後的意義。
原來,這是學生學習數學的一個大障礙!
名稱的改變:-
首先是代數,是以符號代數字,從而達到一般化的運用。卻出現明白3×(4+2)=3×4+3×2,卻不明白 x(y+z)=xy+xz。
然後是最優化,教了學生怎樣求得最大值,他們卻往往未能舉一反三地求出最小值。大與小,很多時只是換個名稱而已!
定義(含義)的不同:-
首先是關係,不同的場合,大小的定義可能完全不同。一般來說,我們會說 4>2>1>-3;但這並非絕對!
在玩橋牌的時候,我們有1>4>2;在玩“鋤大弟”的時候,我們知道 2>1>4。但若我們不提橋牌,不提鋤大弟,而只說 1>4>2 或 2>1>4,學生會頓時不知所措!!!
在物理學中,若以 K 為温度單位,負温度會比正温度為熱。若以>表示比較熱,則有-3>4>2>1!
然後是擴張,隨着認知深化,需要擴張定義符合實況。在初學複數時,學生仍會給舊認知 “沒有「數」的平方是負數” 所跘着,不理解「數」的定義已改變。
在高級代數書中,a1=a=1a並不單是表示數的乘法(a× 1=a=1× a),亦可表示數的加法(a+0=a=0+a),用意是把「乘法」擴張以覆蓋所有性質相近的運算,減省研究的重複性。可想而知,學生多數未能了解。
在中學物理學中,我們是以温度定義冷熱,但大學時,我們以能量流向定義冷熱。
***********************
在文學中,「名」也有難題。在一些文化中,一個人往往有着不同的稱謂,或者一個家族不同人有相同的名稱,令記性不大好的人(如在下)難於閱讀相關傳記或小說!
例如,三國演義中,一人往往有着三個或以上的稱呼,如諸葛亮,字孔明,號臥龍先生;
又如世界首富比爾蓋茨(William Henry Gates III)的父親也是比爾蓋茨(William Henry Gates, Sr.)!
科學與文學中的「名」已這麼難掌握,更何況哲學中的「名」?
Sunday, April 16, 2006
『熱』極必『冷』
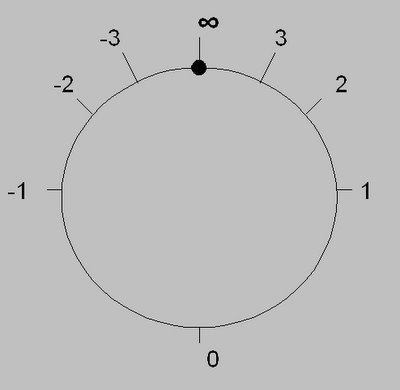
當數線兩端相接,正的盡頭便是負,有中國哲理「物極必反」味道。
物理學上,也有一個古怪現象:若温度不斷提高,在超越無限高温後,温度會變成負數!看來也真有「『熱』極必『冷』」這回事!
但不要給字面騙了,負温度其實比正温度更“熱”!
科學家量度氣温,不是用攝氏 °C 或華氏 °F,而是用開爾文溫標 K。0 K,相當於 -273.15 °C,稱為絕對零度,是低温的極限,一切動能將會消失; 然後1 K = 1 °C,遂級而上,冰點是 273.15 K,太陽表面是 5780 K,太陽中心是 1.3 × 106 K,黑洞温度是1.4×1032 K。
但甚麼是温度?有一個不太簡單的定義是:温度=熵(混亂程度)的變化/能量的變化。一般而言,能量的增加會導致熵的增加,因而有正數的温度;但在某些狀況(最混亂時?),能量增加反而導致熵減少,所以出現負數的温度。
甚麼是冷熱?這是相對的,能量是由較熱處流向較冷處。因為能量會由負温度處流向正温度處,所以負温度比正温度更熱!
當然,我們仍可以用温度的高低來定義冷熱,我們仍可以說「『熱』極必『冷』」,但卻失去如能量流動般的重要物理意義。
Saturday, April 15, 2006
無窮的小
恒古以來,人類便為着物質是無限可分,或有終極結構爭論不休。
古希臘的原子論認為物質是由最小稱為『原子』的東西構成。伴隨着現代化學的誔生,某程度上肯定了原子論。
但化學中的原子,物理學卻仍可分割下去,得出常見的電子、質子、中子,以及μ子、π子、W子、Ω子等等;超弦理論認為還可再分下去,直至達到所謂的超弦結構。
超弦是大小為普朗克單位(Planck units)的物理結構;而普朗克單位,被視為是測量的下限。在普朗克時間(5.39121 × 10-44 s)及普朗克尺度(1.61624 × 10-35 m)內,前與後、左與右亦沒有物理意義。
當前最heat的topic,即納米技術,是以納米(1 nm= 10–9m)為基礎的技術,其實在物理學中不是太小。
普朗克尺度非常小,比佛家的“刹那”還要小,但始終是有限的小,不是『無窮小』。無窮小,是個大於零卻小於任可正數的量,給人難以捉摸的印象;事實上,當數學家最初使用無窮小時,亦困於其邏輯難關,但仍決定實用先行。
當時有名的思想家貝克箂主教對無窮小的應用,作出頗嚴厲的批判;稍後數學家找出方法,可以繞過無窮小,亦令無窮小的議論趨向沈寂。
上世紀中期,Abraham Robinson提出新的數學系統--超實數系統(hyperreal numbers),包含了不同的無限大及無窮小,而且解決了邏輯問題。但沒有無窮小的數學已是主流,新的數學被稱為『非標準分析學』。
在超實數系統中,0.999..... ≠ 1!!!兩數的相差,便是個無窮小。
古希臘的原子論認為物質是由最小稱為『原子』的東西構成。伴隨着現代化學的誔生,某程度上肯定了原子論。
但化學中的原子,物理學卻仍可分割下去,得出常見的電子、質子、中子,以及μ子、π子、W子、Ω子等等;超弦理論認為還可再分下去,直至達到所謂的超弦結構。
超弦是大小為普朗克單位(Planck units)的物理結構;而普朗克單位,被視為是測量的下限。在普朗克時間(5.39121 × 10-44 s)及普朗克尺度(1.61624 × 10-35 m)內,前與後、左與右亦沒有物理意義。
當前最heat的topic,即納米技術,是以納米(1 nm= 10–9m)為基礎的技術,其實在物理學中不是太小。
普朗克尺度非常小,比佛家的“刹那”還要小,但始終是有限的小,不是『無窮小』。無窮小,是個大於零卻小於任可正數的量,給人難以捉摸的印象;事實上,當數學家最初使用無窮小時,亦困於其邏輯難關,但仍決定實用先行。
當時有名的思想家貝克箂主教對無窮小的應用,作出頗嚴厲的批判;稍後數學家找出方法,可以繞過無窮小,亦令無窮小的議論趨向沈寂。
上世紀中期,Abraham Robinson提出新的數學系統--超實數系統(hyperreal numbers),包含了不同的無限大及無窮小,而且解決了邏輯問題。但沒有無窮小的數學已是主流,新的數學被稱為『非標準分析學』。
在超實數系統中,0.999..... ≠ 1!!!兩數的相差,便是個無窮小。
Thursday, April 13, 2006
無限的大
在 《零與空》中,我說把0看作一個空的袋子,而不是空,可把形而上學的味道減至最小。朋友笑說:若是個無限大的袋子,那未不是和虛空一樣嗎?
當然,整個宇宙根本不是無限大,所以沒有無限大的袋子。
其實,『無限大』是甚麼?有信仰的人士可能會說他的神就是無限大,但科學的應用需要的是世俗的無限大。康托爾(Georg Cantor)率先對數學上無限大下定義,並由此創造出集合論。
不同的宗教有不同的神,即使同一宗教也可能有不同等級的神。
除着研究的深入,數學家發現不同的系統有不同的無限,即使同一系統內也可有不同大小的無限。
讓我們先看看康托爾的無限,即由比較多少引申出來的無限:
在《自然的數?》中, 我說 0={ },1={0},2={0,1}, 3={0,1,2},4={0,1,2,3},...。可以見到 0 <1 <2 <3 <4 <5 <...。把所有自然數放在一起,有N={0,1,2,...},得0 < 1 <2 <... <N。
把整條數線列出來(記作c),除自然數外還有很多數字,所以 N < c。 c 當然也是無限。
就這樣,可看到有兩個不同的無限。當然,還可以不停引申下去。
接着,讓我們看看由數字大小引申出的無限:
我們最熟悉的無限莫如 ∞ 及 -∞,是甚麼呢?基本上,這只是兩個符號,∞ 表示比任何正數都正,-∞ 表示比任何負數都負。它倆都不是數,因為不能進行四則運算。而 ∞ 及 -∞ 是數線的兩極,直如祆教中陰陽兩個神衹,有你冇我!

不過若我們把正無窮與負無窮都看作是同一個無限 ∞ ,我們得到一個環,稱為數線的“一點緊化”(one point compactification),就有些中國哲理「物極必反」的味道,因正的盡頭便是負!雖然 ∞ 也是一個無限,但與其他數字都只是環上的一點,失去了某些特殊性。

把無限賦與一般數字性質的是Abraham Robinson,他的系統內有無限個無窮大,若 x,y 是不同的無窮大(即比所有數字都大),則x+2,3y,x+y等,都是不同的無窮大;而-x,-y則是不同的負無窮大(即比所有負數都負);1/x,1/y則是不同的無窮小(即不是0,卻比所有正數都小)。
唔,不論任何情形,都沒有1/0啊!所以盡量不要說1/0=∞!
當然,整個宇宙根本不是無限大,所以沒有無限大的袋子。
其實,『無限大』是甚麼?有信仰的人士可能會說他的神就是無限大,但科學的應用需要的是世俗的無限大。康托爾(Georg Cantor)率先對數學上無限大下定義,並由此創造出集合論。
不同的宗教有不同的神,即使同一宗教也可能有不同等級的神。
除着研究的深入,數學家發現不同的系統有不同的無限,即使同一系統內也可有不同大小的無限。
讓我們先看看康托爾的無限,即由比較多少引申出來的無限:
在《自然的數?》中, 我說 0={ },1={0},2={0,1}, 3={0,1,2},4={0,1,2,3},...。可以見到 0 <1 <2 <3 <4 <5 <...。把所有自然數放在一起,有N={0,1,2,...},得0 < 1 <2 <... <N。
把整條數線列出來(記作c),除自然數外還有很多數字,所以 N < c。 c 當然也是無限。
就這樣,可看到有兩個不同的無限。當然,還可以不停引申下去。
接着,讓我們看看由數字大小引申出的無限:
我們最熟悉的無限莫如 ∞ 及 -∞,是甚麼呢?基本上,這只是兩個符號,∞ 表示比任何正數都正,-∞ 表示比任何負數都負。它倆都不是數,因為不能進行四則運算。而 ∞ 及 -∞ 是數線的兩極,直如祆教中陰陽兩個神衹,有你冇我!

不過若我們把正無窮與負無窮都看作是同一個無限 ∞ ,我們得到一個環,稱為數線的“一點緊化”(one point compactification),就有些中國哲理「物極必反」的味道,因正的盡頭便是負!雖然 ∞ 也是一個無限,但與其他數字都只是環上的一點,失去了某些特殊性。

把無限賦與一般數字性質的是Abraham Robinson,他的系統內有無限個無窮大,若 x,y 是不同的無窮大(即比所有數字都大),則x+2,3y,x+y等,都是不同的無窮大;而-x,-y則是不同的負無窮大(即比所有負數都負);1/x,1/y則是不同的無窮小(即不是0,卻比所有正數都小)。
唔,不論任何情形,都沒有1/0啊!所以盡量不要說1/0=∞!
自然的數?
數是甚麼?由遠古開始,1、2、3、...分別是一種東西、二種東西、三種東西...的量化詞,所以這些才是一般人心中的數。但隨着小數,分數等出現,我們把1、2、3、...稱作自然數,即這些才是自然出現的數。
但數學家需要更堅實的定義。
在《萬『數』皆『集』》中,我說每個數都是一個『集合』--可以看成一個袋子。0是空空如也的袋子,1是載着一件東西的袋子,2是載着兩件東西的袋子,如此類推。
0是空空如也的袋子,記作{}。
既然1是載着一件東西的袋子,內裡的東西是甚麼呢?一個包、一件衫、一張相?都可以,就如西施狗、牧羊狗、狼狗都可以代表狗。於是1可以是{包},可以是{衫},可以是{相},但也可以放進一個0,即{0}!
如此類推,2載着0及1,記作{0,1}。3是{0,1,2},4是{0,1,2,3},5是{0,1,2,3,4}。
這樣,可以不假外求,完全在數學內定義出所有0,1,2,...。這些數,是其他數的起點,就是自然數!問題出現了,0似乎不那麼『自然』,它由誔生至被接受成數字需要經過數百年,怎看也不自然吧?!
現在,若把0當自然數,便把1,2,...稱為正整數;若不把0當自然數,便把0,1,2,...稱作非負整數。夠混亂了罷!
不過1,2,...也並非真的這麼自然,亞馬遜河居住的Pirahã族人,其語文根本沒有數字慨念!--數,既然不是必需,或者根本不能說自然!
或者『自然』也是相對的,一些人的自然是另一些人的不自然。
但數學家需要更堅實的定義。
在《萬『數』皆『集』》中,我說每個數都是一個『集合』--可以看成一個袋子。0是空空如也的袋子,1是載着一件東西的袋子,2是載着兩件東西的袋子,如此類推。
0是空空如也的袋子,記作{}。
既然1是載着一件東西的袋子,內裡的東西是甚麼呢?一個包、一件衫、一張相?都可以,就如西施狗、牧羊狗、狼狗都可以代表狗。於是1可以是{包},可以是{衫},可以是{相},但也可以放進一個0,即{0}!
如此類推,2載着0及1,記作{0,1}。3是{0,1,2},4是{0,1,2,3},5是{0,1,2,3,4}。
這樣,可以不假外求,完全在數學內定義出所有0,1,2,...。這些數,是其他數的起點,就是自然數!問題出現了,0似乎不那麼『自然』,它由誔生至被接受成數字需要經過數百年,怎看也不自然吧?!
現在,若把0當自然數,便把1,2,...稱為正整數;若不把0當自然數,便把0,1,2,...稱作非負整數。夠混亂了罷!
不過1,2,...也並非真的這麼自然,亞馬遜河居住的Pirahã族人,其語文根本沒有數字慨念!--數,既然不是必需,或者根本不能說自然!
或者『自然』也是相對的,一些人的自然是另一些人的不自然。
Monday, April 10, 2006
一個數學故事
在某年某月某日,有兩位學者大膽猜測宇宙中存在一個巨大的怪獸群。要證明他們的猜想,展開了漫長的時空搜索。經過多年的努力,他們穿越了一個一一六八八三維的空間,並成功找出了怪獸群,震撼國際。怪獸群果真異常巨大,內個體數目以億兆計,難以作簡單的描述。
後來,有人認定這怪獸群與傳說中不可思議的『怪異月光』有關,又開始了一個大規模的探索。經過不少的艱辛,流過不少汗水,終於有一天,探究者發現了傳說中的『怪異月光』。
多年後,有兩人在討論怪獸群.一個讚嘆道:『這個怪獸群真是不簡單!』另一人搖頭笑說:『不!這個怪獸群真是簡單!』
故事完。
問:為什麼這是一個數學故事? 如果你還在求學,問問你的數學老師。他可能答錯,但不要取笑他,這可不是個容易答的問題啊!答案如下:
 一群怪獸,但不是一個『怪獸群』:P。
一群怪獸,但不是一個『怪獸群』:P。
群 group 是一個數學結構,擁有乘及除兩種運算。群內有群稱作子群 subgroup,沒有所謂正規子群 normal subgroup 的群就是簡單群 simple group。簡單群的結構一般真的簡單,除了廿六個奇怪簡單群(名為零散群 sporadic groups)之外。
兩位數學家Fischer及Griess在1970億測哪個是最大的零散群,將之定名怪獸群 Monster group。七年後終於證實怪獸群的存在,構作方法是利用一個196883維的代數空間。這個怪獸群有8 × 1053個“元素”,真是非常巨大。
怪異月光 monstrous moonshine 是關於怪獸群的另一個特性,即使研究者亦以「怪異」稱之。由Conway及Norton在1979年提出,在1992年被Borcherds證明──Borcherds亦由此獲得數學界最高榮譽菲爾茲奬。
怪獸群毫不簡單,但它畢竟是個簡單群呀!
後來,有人認定這怪獸群與傳說中不可思議的『怪異月光』有關,又開始了一個大規模的探索。經過不少的艱辛,流過不少汗水,終於有一天,探究者發現了傳說中的『怪異月光』。
多年後,有兩人在討論怪獸群.一個讚嘆道:『這個怪獸群真是不簡單!』另一人搖頭笑說:『不!這個怪獸群真是簡單!』
故事完。
問:為什麼這是一個數學故事? 如果你還在求學,問問你的數學老師。他可能答錯,但不要取笑他,這可不是個容易答的問題啊!答案如下:
 一群怪獸,但不是一個『怪獸群』:P。
一群怪獸,但不是一個『怪獸群』:P。群 group 是一個數學結構,擁有乘及除兩種運算。群內有群稱作子群 subgroup,沒有所謂正規子群 normal subgroup 的群就是簡單群 simple group。簡單群的結構一般真的簡單,除了廿六個奇怪簡單群(名為零散群 sporadic groups)之外。
兩位數學家Fischer及Griess在1970億測哪個是最大的零散群,將之定名怪獸群 Monster group。七年後終於證實怪獸群的存在,構作方法是利用一個196883維的代數空間。這個怪獸群有8 × 1053個“元素”,真是非常巨大。
怪異月光 monstrous moonshine 是關於怪獸群的另一個特性,即使研究者亦以「怪異」稱之。由Conway及Norton在1979年提出,在1992年被Borcherds證明──Borcherds亦由此獲得數學界最高榮譽菲爾茲奬。
怪獸群毫不簡單,但它畢竟是個簡單群呀!
Saturday, April 08, 2006
偽學問:是與非
剛拜讀田松博士的《永动机与哥德巴赫猜想》 ,描述的是全世界科學家的一個惡夢:『民間科學家』。
民間科學家是指一些沒經過正統訓練,以貧乏的知識及不成熟的邏輯思維,希望得出對世界具影嚮力的重大發明。他們嘗試制造永動機(幾乎是無中生有的得到能量),三等分任意角(以知不可能的古希臘數學題),及證明哥德巴赫猜想(當令最知名的數學難題)等等。他們即使無數次被科學家指出其錯誤,但仍頑強地研究,並把批評視為無知或打壓。
民間科學家大多是獨立研究,帶着孤獨前鋒的悲壯;但亦有一些得到廣泛支持,結果發展成偽科學(如雙氧水治病,“神化了的”氣功等)。
當然也有一些因為名氣、金錢、宗教等原因,故意推出違背一般科學知識的理論:如莫札特效應,智慧創造論,採光美容等。事實上,這類偽科學的受支持程度,甚至超乎正統科學。
除科學以外,還有很多相似的情況:有人提出中國人先發現新大陸;工會分子積極挑戰經濟學家的理論;不知所謂的行為藝術家。
不過對這些另類理論的支持者,我們反而是頑固的一群。當是與非的感覺倒置了,是與非真的倒置了麼?
民間科學家是指一些沒經過正統訓練,以貧乏的知識及不成熟的邏輯思維,希望得出對世界具影嚮力的重大發明。他們嘗試制造永動機(幾乎是無中生有的得到能量),三等分任意角(以知不可能的古希臘數學題),及證明哥德巴赫猜想(當令最知名的數學難題)等等。他們即使無數次被科學家指出其錯誤,但仍頑強地研究,並把批評視為無知或打壓。
民間科學家大多是獨立研究,帶着孤獨前鋒的悲壯;但亦有一些得到廣泛支持,結果發展成偽科學(如雙氧水治病,“神化了的”氣功等)。
當然也有一些因為名氣、金錢、宗教等原因,故意推出違背一般科學知識的理論:如莫札特效應,智慧創造論,採光美容等。事實上,這類偽科學的受支持程度,甚至超乎正統科學。
除科學以外,還有很多相似的情況:有人提出中國人先發現新大陸;工會分子積極挑戰經濟學家的理論;不知所謂的行為藝術家。
不過對這些另類理論的支持者,我們反而是頑固的一群。當是與非的感覺倒置了,是與非真的倒置了麼?
Monday, April 03, 2006
絕對與相對
朋友在他的《絕對與相對》,又提出「是」一字可產生的問題。奇實自公孫龍白馬非馬以來,關於「是」「非」的語意岐義,已分析過何只千萬次!
科學上,需要嚴防岐義,所以要創造一些符號語言,可算是人類第一套沒有讀音的文字。
「一支筆是文具」:一支筆∈文具;∈表示「其中一個」。
「筆是文具」:筆⊆文具;⊆表示「其中一種」。
「文學創作工具是文具」:文學創作工具=文具;=表示「等如」。
「百無一用是書生」:百無一用(的東西)⊇ 書生;這其實是倒裝寫法,我懷疑「佛教是文學,哲學,科學」本應寫為「文學,哲學,科學皆是佛學」。
「強人是你,能頂天立地」:強人∋ 你;這也是倒裝法。
當然啦,「是」還有其他用法。
「是其是」:第一個「是」意思為「贊成,支持」,第二個「是」意思為「正確的事」;全句為「贊成正確的事」。
當然啦,此乃我極膚淺的分析。很多時候,文學作者故意利用模棱兩可的觀念創作,這也算留白罷!
或者正如我朋友所說,不要時常太執着於正確的意思:世上多數東西都只有「相對正確」,沒有「絕對正確」。
科學上,需要嚴防岐義,所以要創造一些符號語言,可算是人類第一套沒有讀音的文字。
「一支筆是文具」:一支筆∈文具;∈表示「其中一個」。
「筆是文具」:筆⊆文具;⊆表示「其中一種」。
「文學創作工具是文具」:文學創作工具=文具;=表示「等如」。
「百無一用是書生」:百無一用(的東西)⊇ 書生;這其實是倒裝寫法,我懷疑「佛教是文學,哲學,科學」本應寫為「文學,哲學,科學皆是佛學」。
「強人是你,能頂天立地」:強人∋ 你;這也是倒裝法。
當然啦,「是」還有其他用法。
「是其是」:第一個「是」意思為「贊成,支持」,第二個「是」意思為「正確的事」;全句為「贊成正確的事」。
當然啦,此乃我極膚淺的分析。很多時候,文學作者故意利用模棱兩可的觀念創作,這也算留白罷!
或者正如我朋友所說,不要時常太執着於正確的意思:世上多數東西都只有「相對正確」,沒有「絕對正確」。
意大利粉神教

原教旨基督教的最大對手是誰?
原教旨回教徒?不是,他們沒有像美國般的超級大國撐腰!
其他的基督教派?這不算對手罷,頂多只是教義詮釋不同而已!
告訴你吧,是意大利粉神教(Church of the Flying Spaghetti Monsterism)。噢,未聽過?它的每個教義都衝着神創論(Creationism,新稱智慧設計論 Intelligent Design)而來。
據說每個支持智慧設計論的證據,都可以支持意大利粉神教。
該教派已向美國各州政府發公開信:美國學校的生物科若要教授智慧設計論,作為進化論的代替理論,則應同時教授意大利粉神教。
若閣下已開始厭倦『訓教』,是時候考慮意大利粉神教,總比信飛碟教(真道教)好,起碼不用作出金錢奉獻!(哈哈!)
註:若此篇文章令基督徒感覺冒犯,請多多吃意大利粉及多多包涵!
Sunday, April 02, 2006
科學與宗教
語文是非常奇怪的東西,同一句說話,可以有極端不同的意思。
在上一篇我認為可以說「科學是佛教」,不可以說「佛教是科學」;我的朋友旋即撰文反對,但似乎只是誤解。
他認為科學是佛教的一部分,並非全部,所以不好說「科學是佛教」;但「白馬是馬」,「西施狗是狗」,「量子力學是物理」,其中的「是」都意味着「部分」。
他認為「佛教是科學」並無不妥,而且佛教同時是文學及哲學;但他心中的「是」意義是「包容」,不過我也聽過一些信徒說「因為佛教是科學,所以可信」。
心境不同,層次不同,使得一句說話有不同的意思。
宗教與科學的關係,千絲萬縷:化學源於煉金術,天文始於星相學,宗教可促進科學;教廷曾封殺日心說,全屍觀念不容解剖學,宗教亦可扯科學後腿。找出平衡絕非易事!
若一些科學理論與宗教觀念不相容,提倡者經常被斥為異端。例如:進化論者常被原教旨基督教徒視為無神論者,雖然有不少進化論者是基督徒(參看www.talkorigins.org)。
真正視科學為絕對的應是唯物論者,他們認為心靈也是由物質所決定。當然唯物論也可算是一種信仰。
不要混淆科學教派(scientology),它的教義雖說相信科學,但它所相信的“科學”被多數學者歸類為偽科學!
在上一篇我認為可以說「科學是佛教」,不可以說「佛教是科學」;我的朋友旋即撰文反對,但似乎只是誤解。
他認為科學是佛教的一部分,並非全部,所以不好說「科學是佛教」;但「白馬是馬」,「西施狗是狗」,「量子力學是物理」,其中的「是」都意味着「部分」。
他認為「佛教是科學」並無不妥,而且佛教同時是文學及哲學;但他心中的「是」意義是「包容」,不過我也聽過一些信徒說「因為佛教是科學,所以可信」。
心境不同,層次不同,使得一句說話有不同的意思。
宗教與科學的關係,千絲萬縷:化學源於煉金術,天文始於星相學,宗教可促進科學;教廷曾封殺日心說,全屍觀念不容解剖學,宗教亦可扯科學後腿。找出平衡絕非易事!
若一些科學理論與宗教觀念不相容,提倡者經常被斥為異端。例如:進化論者常被原教旨基督教徒視為無神論者,雖然有不少進化論者是基督徒(參看www.talkorigins.org)。
真正視科學為絕對的應是唯物論者,他們認為心靈也是由物質所決定。當然唯物論也可算是一種信仰。
不要混淆科學教派(scientology),它的教義雖說相信科學,但它所相信的“科學”被多數學者歸類為偽科學!
Friday, March 31, 2006
社會“科學”?
教育學、經濟學、政治學,都屬於社會學範籌,擁有同一特點:實驗難!
準確點說,是控制實驗難。為甚麼呢?
首先,一些實驗的道德問題太大--舉例說,有理論說如何如何一個人會破產,或如何如何一個人會變成罪犯,可以做實驗證明嗎?相反,有理論說如何如何一間公司會發展得更好,或如何如何一個兒童會成長得更好,有多少老闆或家長會冒着理論錯誤的風險做實驗?
其次,一個完美的科學實驗,要令得變數愈少愈好--例如要知道重量及壓力的關係,就要保持溫度不變,以免把問題複雜化。但與人有關的事,這可以做到嗎?
最後,變數太多--即使結果與實驗不同,也難知是理論錯,還是其他環節出錯!人往往是頑固的,不承認是理論錯,並諉過於其他。這導致理論發展的困難。
第三點,其實才是最致命的弱點。現代科學家多根據卡爾·波普爾(Karl Popper)的說法,認為只有一個理論是可偽證的,即有機會被證明是錯的,才算是科學(science)!
占卜、氣功、風水,相關的專家往往不肯「認低威」--這也難怪,理論錯誤會丟飯碗--所以很難成為被接受的科學。
有很多宗教信徒,常說自己的宗教是科學,卻其實犯了兩個錯誤:一個大錯,及一個極大錯。
大錯是宗教不可能偽證,諸如不可能用實驗測試神是否存在,所以不是科學--但這只是與現代科學定義相悖而已。
極大錯是把宗教置於科學之下!科學是希望用『理論模型』以解釋自然現象,而可偽證表明這未必是絕對的。所以稱宗教為科學根本不能證明宗教的正確性!宗教之所以稱為信仰,是以『信心』為主,不應該要證明!
若然相信科學,應該把科學包含於宗教之內,而不是倒轉。我們可以說「科學是回教」,「科學是佛教」,但絕不可說「回教是科學」,「佛教是科學」!
互聯網的出現,給社會學一個做實驗的機會。虛擬社區,便是簡化了的社會模型!網上遊戲The Sims Online,已成為社會學家一個有趣的觀察平台。由此,社會學可名正言順的稱為社會科學(social science)。
準確點說,是控制實驗難。為甚麼呢?
首先,一些實驗的道德問題太大--舉例說,有理論說如何如何一個人會破產,或如何如何一個人會變成罪犯,可以做實驗證明嗎?相反,有理論說如何如何一間公司會發展得更好,或如何如何一個兒童會成長得更好,有多少老闆或家長會冒着理論錯誤的風險做實驗?
其次,一個完美的科學實驗,要令得變數愈少愈好--例如要知道重量及壓力的關係,就要保持溫度不變,以免把問題複雜化。但與人有關的事,這可以做到嗎?
最後,變數太多--即使結果與實驗不同,也難知是理論錯,還是其他環節出錯!人往往是頑固的,不承認是理論錯,並諉過於其他。這導致理論發展的困難。
第三點,其實才是最致命的弱點。現代科學家多根據卡爾·波普爾(Karl Popper)的說法,認為只有一個理論是可偽證的,即有機會被證明是錯的,才算是科學(science)!
占卜、氣功、風水,相關的專家往往不肯「認低威」--這也難怪,理論錯誤會丟飯碗--所以很難成為被接受的科學。
有很多宗教信徒,常說自己的宗教是科學,卻其實犯了兩個錯誤:一個大錯,及一個極大錯。
大錯是宗教不可能偽證,諸如不可能用實驗測試神是否存在,所以不是科學--但這只是與現代科學定義相悖而已。
極大錯是把宗教置於科學之下!科學是希望用『理論模型』以解釋自然現象,而可偽證表明這未必是絕對的。所以稱宗教為科學根本不能證明宗教的正確性!宗教之所以稱為信仰,是以『信心』為主,不應該要證明!
若然相信科學,應該把科學包含於宗教之內,而不是倒轉。我們可以說「科學是回教」,「科學是佛教」,但絕不可說「回教是科學」,「佛教是科學」!
互聯網的出現,給社會學一個做實驗的機會。虛擬社區,便是簡化了的社會模型!網上遊戲The Sims Online,已成為社會學家一個有趣的觀察平台。由此,社會學可名正言順的稱為社會科學(social science)。
Wednesday, March 29, 2006
有教無類
與一位資深人士談天,認為教育署提倡『融合教育』 - 把殘障學生放入一般學校 - 是好心做壞事,被虛無的『有教無類』害苦了。
但『有教無類』,是指對所有學生都同樣的用心去教,而不是指對所有學生都用同樣方法來教!有教無類,若不能配合『因材施教』,當然事倍功半!
現實是,根本沒有學校有足夠資源來因材施教,一般學生因程度不同產生的問題也難解決,所以我們才要把學生分級。至於標籤效應,是無奈的社會現實。
融合教育,和把學生分級相反,是把有不同需要的學生放在一起,這當然要投入大量資源,但這究竟符不符合社會效益?
或者,鼓勵不同學校(包括一般學校,特殊學校,及其他)多作課外交流,會不會是個更好的選擇?
作為研究,教育理論是最困難。大多數教育理論都是紙上談兵,沒有多少實驗數據支持;皆因那個家長會在有其他可行方法的情況下,容許自己的孩子作實驗室的白老鼠?除非是政府帶頭作試驗,但一不小心,就是政治事件,香港的教育改革便是證明!
在社會學的其他範圍,因互聯網的出現而令實驗變得可行,在虛擬世界可容易創造出不同的網上社會;但教育理論的測試,目前仍可說是舉步為艱!
但『有教無類』,是指對所有學生都同樣的用心去教,而不是指對所有學生都用同樣方法來教!有教無類,若不能配合『因材施教』,當然事倍功半!
現實是,根本沒有學校有足夠資源來因材施教,一般學生因程度不同產生的問題也難解決,所以我們才要把學生分級。至於標籤效應,是無奈的社會現實。
融合教育,和把學生分級相反,是把有不同需要的學生放在一起,這當然要投入大量資源,但這究竟符不符合社會效益?
或者,鼓勵不同學校(包括一般學校,特殊學校,及其他)多作課外交流,會不會是個更好的選擇?
作為研究,教育理論是最困難。大多數教育理論都是紙上談兵,沒有多少實驗數據支持;皆因那個家長會在有其他可行方法的情況下,容許自己的孩子作實驗室的白老鼠?除非是政府帶頭作試驗,但一不小心,就是政治事件,香港的教育改革便是證明!
在社會學的其他範圍,因互聯網的出現而令實驗變得可行,在虛擬世界可容易創造出不同的網上社會;但教育理論的測試,目前仍可說是舉步為艱!
Tuesday, March 21, 2006
類同,同類
峰人風語在《另外與例外》中,以為alternative一詞把「另類」的概念演繹得很出色。但中文的「類」字本身亦很有趣:放於名詞之後,便可引為同類;放於名詞之前,便是似而不同。
類人猿是像人的猿。
類白蛋是似蛋白質的化合物。
類星體是似星星(恒星)的太空物體。
不知類固醇名稱由來?
如果我們不說「偽科學」或「偽氣功」,而說「類科學」或「類氣功」,會否厚道一點?
正如我們不說「假唐三彩」,而說「仿唐三彩」,總之要人知道不是「唐三彩」便成了!
若我們說中國是「類民主」,而非「假民主」,領導人會否順氣點?
突然感想:其實香港學生早知求學不是求「分數」,而是求「分類」 - 考試成績是A類、B類、C類、...、F類;學業成績是Band 1 類、Band 2 類、Band 3 類;大學畢業是一級榮譽類、二級榮譽類、三級榮譽類;等等....唉!這和有教無類是否背道而馳?
類人猿是像人的猿。
類白蛋是似蛋白質的化合物。
類星體是似星星(恒星)的太空物體。
不知類固醇名稱由來?
如果我們不說「偽科學」或「偽氣功」,而說「類科學」或「類氣功」,會否厚道一點?
正如我們不說「假唐三彩」,而說「仿唐三彩」,總之要人知道不是「唐三彩」便成了!
若我們說中國是「類民主」,而非「假民主」,領導人會否順氣點?
噢,這篇文章類同無厘頭,實與廢話同類!
突然感想:其實香港學生早知求學不是求「分數」,而是求「分類」 - 考試成績是A類、B類、C類、...、F類;學業成績是Band 1 類、Band 2 類、Band 3 類;大學畢業是一級榮譽類、二級榮譽類、三級榮譽類;等等....唉!這和有教無類是否背道而馳?
Saturday, March 18, 2006
物以類聚
上篇《抽象的無厘頭》談及數學中稱為『類』的概念,不容易理解。
其實不論在任何學問,分類也是個難搞的問題。不良的分類系統,會令研究、分析、及應用變得因難。而隨着社會及認知的改變,分類系統亦要與時俱進。
最常接觸的分類問題,首選市埸學。若在糧油雜貨的地方賣書,可能只是笑話而已;但若在公共屋邨經營高級時裝店,不虧本才怪!
圖書館學當然以分類學為核心,不過金融數學的書應放在金融學還是數學的書架呢?
化學的分類,以往建基於外形特質,現在改由分子結構決定。化學最基本的是原子,目前以原子結構(電子分佈)排列,叫作元素周期表。一般元素周期表是二維平面,其實可以是個三維立體:
生物學的分類,其轉變之速令人詫異,這歸功於突飛猛進的DNA序列科技。誰估到蹄免(hyrax,下圖)竟與大象是近親?

語言分類學的分類亦不容易,苗族和瑤族的語言,是漢藏語系的分支,或是獨立語系,亦有很大爭議。
當然所有的分類學中,最最最困難的是把人分類,皆因隨時可引致岐視或沖突。香港政府把學生分為五級或三級,已可以成為社會問題,這就是明證罷。
其實不論在任何學問,分類也是個難搞的問題。不良的分類系統,會令研究、分析、及應用變得因難。而隨着社會及認知的改變,分類系統亦要與時俱進。
最常接觸的分類問題,首選市埸學。若在糧油雜貨的地方賣書,可能只是笑話而已;但若在公共屋邨經營高級時裝店,不虧本才怪!
圖書館學當然以分類學為核心,不過金融數學的書應放在金融學還是數學的書架呢?
化學的分類,以往建基於外形特質,現在改由分子結構決定。化學最基本的是原子,目前以原子結構(電子分佈)排列,叫作元素周期表。一般元素周期表是二維平面,其實可以是個三維立體:

生物學的分類,其轉變之速令人詫異,這歸功於突飛猛進的DNA序列科技。誰估到蹄免(hyrax,下圖)竟與大象是近親?

語言分類學的分類亦不容易,苗族和瑤族的語言,是漢藏語系的分支,或是獨立語系,亦有很大爭議。
當然所有的分類學中,最最最困難的是把人分類,皆因隨時可引致岐視或沖突。香港政府把學生分為五級或三級,已可以成為社會問題,這就是明證罷。
Friday, March 17, 2006
抽象的無厘頭
所謂萬數皆集,現今數學已可把大部分的數學物件轉化為「集合」-簡單來說,集合就是一堆堆東西。
而然,因邏輯原因,不能隨便把東西放在一起成為集合。例如沒有包含所有集合的集合。
基於同一原因,不能隨意把同類的集合放在一起成為新的集合。但數學家仍希望把同類的集合放在一起研究,於是他們把同類的集合放在一起,組成一個新的數學物件 - 「類」(class)。
『凡事都有例外』。類,作為數學物件,並不是集合。因為邏輯限制,類的應用比集合論困難;類的抽象,使得多數時候,還是要回歸集合論以解決問題。
但掌握了類,則大大增強數學的深層認知。
因為類的邏輯比集合的邏輯更難,類的抽象比集合的抽象更難掌握,類理論被謔稱為『抽象的無厘頭』(Abstract nonsense)。
抽象的無厘頭,與笑匠周星馳的無厘頭一樣,是有的放矢,要經過精心計算的!
而然,因邏輯原因,不能隨便把東西放在一起成為集合。例如沒有包含所有集合的集合。
基於同一原因,不能隨意把同類的集合放在一起成為新的集合。但數學家仍希望把同類的集合放在一起研究,於是他們把同類的集合放在一起,組成一個新的數學物件 - 「類」(class)。
『凡事都有例外』。類,作為數學物件,並不是集合。因為邏輯限制,類的應用比集合論困難;類的抽象,使得多數時候,還是要回歸集合論以解決問題。
但掌握了類,則大大增強數學的深層認知。
因為類的邏輯比集合的邏輯更難,類的抽象比集合的抽象更難掌握,類理論被謔稱為『抽象的無厘頭』(Abstract nonsense)。
抽象的無厘頭,與笑匠周星馳的無厘頭一樣,是有的放矢,要經過精心計算的!
Tuesday, March 14, 2006
萬『數』皆『集』
道家曰:萬物為一。
佛家曰:萬法皆空。
數學家曰:萬數皆集!
道家及佛家的說法是以形而上學解答問題;數學家剛好相反,是希望避免形而上學。
在文明之初:數目生於實用,圖形始於美學;
隨時間演進:建築、天文、農耕、稅收等,產生新的數學,亦把各種數學枝派連繫起來;
宗教的數學:由天文與占卜,把數學引入宗教內;古希臘人,古印度教,古馬雅,以及易經等,都把數學賦與一定的神秘地位;
科技的發展:經濟及科技的火速發展,令數學的重要性大大增加,亦令『數學是甚麼?』的問題愈趨迷惑。而各種數學枝派,卻未能有效的連繫,冀望有一套共同的數學語言。
集合,是數學家康托爾為研究無限所創造的概念。簡單來說,一個集合就是一堆東西。小學生也懂的温氏圖(見下圖),就是集合的最簡單表逹法。
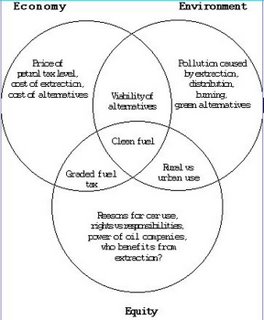
集合所載的,不用是實物:可以是一個個的數字,可以是一種種的思想,可以是一層層的概念。
慢慢地,數學家把幾乎所有的抽象數學物件,變成了一個個的集合。譬如上一篇《零與空》,便提到0是一個甚麼都沒有的集合。集合論的語言,逐步成為所有數學的共同語言。
『數學是甚麼?』在很多時候,都可變成『集合是甚麼?』。集合,就是一堆東西,看來是個非常堅實而簡明的概念,而絕大多數數學家,都可以安安樂樂的,不需要再考慮形而上學的問題。
但危險卻出現,這就是羅素悖論,最形象化的是如下問題:一個「要給所有不自已理髮的人理髮,不給任何自己理髮的人理髮」的理髮師,會不會為自己理髮?
這個例子,生動的說明不是所有的條件都可以運用;對數學來說,即不是隨便把東西放在一起,邏輯上就可以行得通。
二十世紀初的殺着,就是公理化 - 所有數學定理,由最基本的數條『公理』(即可行假設)經邏輯推論而來。於是數學變成了純粹的推理遊戲,杜絕了除便給與條件的運用問題;同時解決『集合是甚麼?』,答案是一些符號而已!
對於最深入的哲理問題,當然仍有哲學家及基礎數學家在努力鑽研(他們認為集合論仍有一些缺點,需要替代或改良)。但『萬數皆集』已是目前最一般的共識!
佛家曰:萬法皆空。
數學家曰:萬數皆集!
道家及佛家的說法是以形而上學解答問題;數學家剛好相反,是希望避免形而上學。
在文明之初:數目生於實用,圖形始於美學;
隨時間演進:建築、天文、農耕、稅收等,產生新的數學,亦把各種數學枝派連繫起來;
宗教的數學:由天文與占卜,把數學引入宗教內;古希臘人,古印度教,古馬雅,以及易經等,都把數學賦與一定的神秘地位;
科技的發展:經濟及科技的火速發展,令數學的重要性大大增加,亦令『數學是甚麼?』的問題愈趨迷惑。而各種數學枝派,卻未能有效的連繫,冀望有一套共同的數學語言。
集合,是數學家康托爾為研究無限所創造的概念。簡單來說,一個集合就是一堆東西。小學生也懂的温氏圖(見下圖),就是集合的最簡單表逹法。

集合所載的,不用是實物:可以是一個個的數字,可以是一種種的思想,可以是一層層的概念。
慢慢地,數學家把幾乎所有的抽象數學物件,變成了一個個的集合。譬如上一篇《零與空》,便提到0是一個甚麼都沒有的集合。集合論的語言,逐步成為所有數學的共同語言。
『數學是甚麼?』在很多時候,都可變成『集合是甚麼?』。集合,就是一堆東西,看來是個非常堅實而簡明的概念,而絕大多數數學家,都可以安安樂樂的,不需要再考慮形而上學的問題。
但危險卻出現,這就是羅素悖論,最形象化的是如下問題:一個「要給所有不自已理髮的人理髮,不給任何自己理髮的人理髮」的理髮師,會不會為自己理髮?
這個例子,生動的說明不是所有的條件都可以運用;對數學來說,即不是隨便把東西放在一起,邏輯上就可以行得通。
二十世紀初的殺着,就是公理化 - 所有數學定理,由最基本的數條『公理』(即可行假設)經邏輯推論而來。於是數學變成了純粹的推理遊戲,杜絕了除便給與條件的運用問題;同時解決『集合是甚麼?』,答案是一些符號而已!
對於最深入的哲理問題,當然仍有哲學家及基礎數學家在努力鑽研(他們認為集合論仍有一些缺點,需要替代或改良)。但『萬數皆集』已是目前最一般的共識!
Saturday, March 11, 2006
零與空
『空』是甚麼?
這是個哲學問題,我不懂答,亦不敢答。
『零』是甚麼?
這是個似乎是相類的哲學問題,但...
在最最最初的時候,0只是用以區分 70 及 700 等數字的符號。
隨着負數的引入,加減乘除的法則往往要根據數值的正負來分類,《九章算經》便是一例。把0作數字看待,便可大大簡化四則運算的規則。事實上,確是意大利商人為着會計便利,不顧統治者對羅馬數字的眷戀,大力推動阿拉伯數字-包括0-的應用。在此,我們要向歷史上最早的會計師致敬!
但,正數代表擁有,負數代表欠缺,0呢?0代表沒有,但既然沒有,又何需代表!
對印度教,佛教,或道教,『有』與『沒有』只是事實的兩面,倒沒甚大不了。
對馬雅人,他們沒有正負數的認知,但他們認為第0日是世界終結或開始,可不容易應付。他們0的符號,倒是最美麗的!

馬雅文化其中兩個0的符號
對中古時的歐洲人,『神』是『創造』,是『有』;『沒有』不是和神相反嗎?
不明白,但好用,0是在爭議聲中成為數學重要的一員。
幸好,數學家有一個解決方法,在公理代系統內,把0看作是自然數的起始點 - 簡單點說,0只是個數學符號而已,會因應不同實際用途給與不同意義。其他自然數1,2,3等,亦作如是觀。畢竟,1,2,3等並非存在於俗世的東西。
溤‧諾伊曼(John von Neumann)提出把0定義為『空集』,這是一個數學慨念,但可以實體化的看作是『空空如也的袋子』:注意是『空空如也的袋子』,不是『空空如也』!
如貴婦狗、狼狗、西施狗,都可稱為狗;空的袋、空的碗、空的錢包,都可喚作零!
這雖不能解決所有問題,但已可解決大多數的問題。
所以0不是『沒有』,亦不是『無』,也不是『空』。
我不是玩弄文字遊戲,日常的『沒有』,道教的『無』,及佛學的『空』,是三個不同的慨念啊!
這是個哲學問題,我不懂答,亦不敢答。
『零』是甚麼?
這是個似乎是相類的哲學問題,但...
在最最最初的時候,0只是用以區分 70 及 700 等數字的符號。
隨着負數的引入,加減乘除的法則往往要根據數值的正負來分類,《九章算經》便是一例。把0作數字看待,便可大大簡化四則運算的規則。事實上,確是意大利商人為着會計便利,不顧統治者對羅馬數字的眷戀,大力推動阿拉伯數字-包括0-的應用。在此,我們要向歷史上最早的會計師致敬!
但,正數代表擁有,負數代表欠缺,0呢?0代表沒有,但既然沒有,又何需代表!
對印度教,佛教,或道教,『有』與『沒有』只是事實的兩面,倒沒甚大不了。
對馬雅人,他們沒有正負數的認知,但他們認為第0日是世界終結或開始,可不容易應付。他們0的符號,倒是最美麗的!


馬雅文化其中兩個0的符號
對中古時的歐洲人,『神』是『創造』,是『有』;『沒有』不是和神相反嗎?
不明白,但好用,0是在爭議聲中成為數學重要的一員。
幸好,數學家有一個解決方法,在公理代系統內,把0看作是自然數的起始點 - 簡單點說,0只是個數學符號而已,會因應不同實際用途給與不同意義。其他自然數1,2,3等,亦作如是觀。畢竟,1,2,3等並非存在於俗世的東西。
溤‧諾伊曼(John von Neumann)提出把0定義為『空集』,這是一個數學慨念,但可以實體化的看作是『空空如也的袋子』:注意是『空空如也的袋子』,不是『空空如也』!
如貴婦狗、狼狗、西施狗,都可稱為狗;空的袋、空的碗、空的錢包,都可喚作零!
這雖不能解決所有問題,但已可解決大多數的問題。
所以0不是『沒有』,亦不是『無』,也不是『空』。
我不是玩弄文字遊戲,日常的『沒有』,道教的『無』,及佛學的『空』,是三個不同的慨念啊!
Thursday, March 09, 2006
不存在的『空間』
半杯水,可以看作一半滿或一半空,視乎觀點學⻆度。不過那一半空間,事實充滿水蒸氣。
『留白 』,可以視作在佈滿色彩的作品中留下一點兒空白,但其實也是在空白的紙張上加一點色彩。不過白色,也是一種顏色。
太空,有一個個獨立星系放在太虛中,但從極大尺度看,也可以是一個個空洞放入充滿物質的世界中。不過有人相信宇宙主要由看不見的暗物質組成,亦相信真空其實充滿瞬間消失的虛粒子。
如是,並沒有真正的空間。『空』,可能只存在於我們的思想之中。
說得太多『空』,自己也開始覺得空洞。不若我們一說另類的空間,數學的空間。
數學中,一堆『物件』加上某種聯系,便可稱為空間。例如平面空間便是{(x,y) : x,y ∈ ℜ} 配上加法 (x,y)+(w,z)=(x+w,y+z) 及距離 ((x-w)2+(y-z)2)1/2。
單獨看,數學空間好像不代表甚麼,但在實際應用時,有不同的意義:歐基里德空間-牛頓物理中,『物件』代表一個個時空的位置;慨率空間-計算機會時,『物件』是一件件可能發生的事;希爾伯特空間-量子力學裡,『物件』是粒子的不同狀態。
但若然拋開它的實用意義,數學空間是甚麼呢?
有一派認為所有數學物件都是真實存在(數學存在主義 Mathematical Realism)。
或者,最最最簡單的,數學空間只是研究結構的一種語言及一種思考方式!
『留白 』,可以視作在佈滿色彩的作品中留下一點兒空白,但其實也是在空白的紙張上加一點色彩。不過白色,也是一種顏色。
太空,有一個個獨立星系放在太虛中,但從極大尺度看,也可以是一個個空洞放入充滿物質的世界中。不過有人相信宇宙主要由看不見的暗物質組成,亦相信真空其實充滿瞬間消失的虛粒子。
如是,並沒有真正的空間。『空』,可能只存在於我們的思想之中。
說得太多『空』,自己也開始覺得空洞。不若我們一說另類的空間,數學的空間。
數學中,一堆『物件』加上某種聯系,便可稱為空間。例如平面空間便是{(x,y) : x,y ∈ ℜ} 配上加法 (x,y)+(w,z)=(x+w,y+z) 及距離 ((x-w)2+(y-z)2)1/2。
單獨看,數學空間好像不代表甚麼,但在實際應用時,有不同的意義:歐基里德空間-牛頓物理中,『物件』代表一個個時空的位置;慨率空間-計算機會時,『物件』是一件件可能發生的事;希爾伯特空間-量子力學裡,『物件』是粒子的不同狀態。
但若然拋開它的實用意義,數學空間是甚麼呢?
有一派認為所有數學物件都是真實存在(數學存在主義 Mathematical Realism)。
或者,最最最簡單的,數學空間只是研究結構的一種語言及一種思考方式!
Friday, March 03, 2006
你沒有留白!
有朋友笑說我上篇《美麗的『空白』》中沒有留白。當然囉,我在文章中說留白要有功力,但我的功力不夠嘛!
或者可能我的風格太學術性 - 學術性文章一般較注重細節;注重細節則沒有多少留白的餘地;沒有留白或者規限了讀者的思想;規限了思想便會沉悶!
但為甚麼有些人對學術性文章看得津津有味呢?
我的答案是:因為他們本身已有一定基礎,容易產生共鳴,在腦海中自動形成思想空間,即是自助『留白』!
舉例說:弗洛伊德的《夢的解析》及馬克思的《資本論》都是經典,但究竟有多少非學者真的看過?
相似的,對大多數學生,數學證明令人頭痛,但偏偏數學家口中有『美麗的證明』。
還有:吵耳的中國戲曲很悅耳,醜陋的昆蟲(以至蟑螂)很有趣,擠迫的建築群很有草根風味,等等。
最懂得留白的是政客,他們時常開空頭支票,給人無限憧憬...
或者可能我的風格太學術性 - 學術性文章一般較注重細節;注重細節則沒有多少留白的餘地;沒有留白或者規限了讀者的思想;規限了思想便會沉悶!
但為甚麼有些人對學術性文章看得津津有味呢?
我的答案是:因為他們本身已有一定基礎,容易產生共鳴,在腦海中自動形成思想空間,即是自助『留白』!
舉例說:弗洛伊德的《夢的解析》及馬克思的《資本論》都是經典,但究竟有多少非學者真的看過?
相似的,對大多數學生,數學證明令人頭痛,但偏偏數學家口中有『美麗的證明』。
還有:吵耳的中國戲曲很悅耳,醜陋的昆蟲(以至蟑螂)很有趣,擠迫的建築群很有草根風味,等等。
最懂得留白的是政客,他們時常開空頭支票,給人無限憧憬...
Tuesday, February 28, 2006
美麗的『空白』
美麗,有不同的定義。能給與觀賞者遐想的空間,也是一種美麗 - 這就是所謂「留白」罷!
留白的意思,在於以最少的內容帶出創作者的思想;給觀賞者足夠想像空間之餘,又不致偏離作者的原意。
留白,太小則成了死板陳述,太大則可能空洞乏味。所以留白絕對顯示創作者的實力。

中國的水墨畫,講求「自然」,要以留白表達道的思想;左圖是八大山人的作品,是典形的水墨畫作。
圖畫有留白,還有其他的留白:
現代舞,有點近乎『不立文字』的境界;但筆者往往功力不夠,不能了解舞者的意思。
寫文章,有所謂「不要畫公仔畫出腸」,最好能做到『書不盡言,言不盡意』。
城市規劃,要有『公共空間』;足夠的空間,才會讓人住得舒服。敢問多位地產公司高層,有住在自己公司起的樓盤嗎?
家居擺設,不要弄得水泄不通,這對空氣流通及家居安全不好。
撰寫法律,也不要寫得太死,這就是『創造性含糊』(creative ambiguity)。
留白的意思,在於以最少的內容帶出創作者的思想;給觀賞者足夠想像空間之餘,又不致偏離作者的原意。
留白,太小則成了死板陳述,太大則可能空洞乏味。所以留白絕對顯示創作者的實力。

中國的水墨畫,講求「自然」,要以留白表達道的思想;左圖是八大山人的作品,是典形的水墨畫作。
圖畫有留白,還有其他的留白:
現代舞,有點近乎『不立文字』的境界;但筆者往往功力不夠,不能了解舞者的意思。
寫文章,有所謂「不要畫公仔畫出腸」,最好能做到『書不盡言,言不盡意』。
城市規劃,要有『公共空間』;足夠的空間,才會讓人住得舒服。敢問多位地產公司高層,有住在自己公司起的樓盤嗎?
家居擺設,不要弄得水泄不通,這對空氣流通及家居安全不好。
撰寫法律,也不要寫得太死,這就是『創造性含糊』(creative ambiguity)。
Sunday, February 26, 2006
最美麗的方程式
大數學家歐拉(Euler)發現的方程式
ei π+1=0
譽為最美麗的方程式,因為它包含了五個最基本(或最重要)的數學單元:歐拉數e,虛單位i,圓周率 π,1 和 0。
注意:黃金比例φ並不包括在內,事實上黃金比例在純數學中的應用相對有限。
歐拉數的命名,是要表彰歐拉對這個特別數字的研究。歐拉數以e代表,也是由歐拉開始(但以乎並非蓄意利用自己名字的首字母)。e在數學的地位,與它在坊間數學小品的罕見,似乎不成比例;一般人要在高等數學才開始接觸e,可能是一個原因,但其實e與香港人的生活息息相關。
當本金為1,年息為1,逐年計算,一年後本利和是 (1+1)1=2;
逐月計算,一年後本利和是(1+1/12)12=2.613;
逐日計算,一年後本利和是(1+1/365)365=2.714;
逐秒計算,一年後本利和是(1+1/525600)525600=2.71828278721;
如是都,把計算的時距不斷縮窄,極限的本利和就是e=2.7182818...
當本金為A,年息為r,一年後的極限本利和就是 A er。可以想像到,所有的金融生工具都與e有關!
直至高中,課本都說所有數字的平方都是正數;所以只有『子虛烏有的數』,即虛數(imaginary number)才可能是 -1 的平方根,記作 i。古代的數學家不想面對這樣的數,但它不斷在數學中出現,逃避不了;直至把 i 等同平面上 (0,1) 這一點,數學家終於擺脫迷思,得出一個二維的數字系統。
可以見到,這是一個革命性的新數字系統,有很多在一維數線上不可能的特性 - 例如正弦(sine)竟然可超過 1!虛數的應用更加進入了物理學,但不時以j代替i,以免與電流符號混淆。
圓周率 π 是圓形的周長與真徑之比,其用途及重要性不用多說。由最古老的『周三徑一』(即 φ=3)到現代準確度達百萬位的計算,關於 π 的故事幾可平行於人類歷史!令人迷惑的是,古人憑甚麼斷定圓周是 2 π r 及圓面積是 π r2?
計算π有很多方法,其中一個有趣的方法是
π/2 = (2/1)(2/3)(4/3)(4/5)(6/5)(6/7)(8/7)(8/9)...
理論上可以由此把π計出來,但要很久很久很久...(打呵欠)。
1 當然重要,它是我們第一個學習的數字呀!其實 1 應該是最常用的數字罷。究竟「一」的概念是否在天生的,亦存在爭議。當然在哲學層面1也是重要的,有所謂『萬法歸一』嘛!
0 的重要性,亦不用多說。但 0 是甚麼,卻不好解釋。自 0 作為位置符號(例:用以區分17或107)面世,以至被接受成數字,它的歷史充滿着哲學和實用的比拼 - 畢竟把「零」、「無」、「道」、「空」四個概念混淆仍大有人在。
最後,如果閣下是在找尋『最美麗容貎的方程式』,這篇文章標題可能誤導了你,請容筆者說句「對不起」。
譽為最美麗的方程式,因為它包含了五個最基本(或最重要)的數學單元:歐拉數e,虛單位i,圓周率 π,1 和 0。
注意:黃金比例φ並不包括在內,事實上黃金比例在純數學中的應用相對有限。
歐拉數的命名,是要表彰歐拉對這個特別數字的研究。歐拉數以e代表,也是由歐拉開始(但以乎並非蓄意利用自己名字的首字母)。e在數學的地位,與它在坊間數學小品的罕見,似乎不成比例;一般人要在高等數學才開始接觸e,可能是一個原因,但其實e與香港人的生活息息相關。
當本金為1,年息為1,逐年計算,一年後本利和是 (1+1)1=2;
逐月計算,一年後本利和是(1+1/12)12=2.613;
逐日計算,一年後本利和是(1+1/365)365=2.714;
逐秒計算,一年後本利和是(1+1/525600)525600=2.71828278721;
如是都,把計算的時距不斷縮窄,極限的本利和就是e=2.7182818...
當本金為A,年息為r,一年後的極限本利和就是 A er。可以想像到,所有的金融生工具都與e有關!
直至高中,課本都說所有數字的平方都是正數;所以只有『子虛烏有的數』,即虛數(imaginary number)才可能是 -1 的平方根,記作 i。古代的數學家不想面對這樣的數,但它不斷在數學中出現,逃避不了;直至把 i 等同平面上 (0,1) 這一點,數學家終於擺脫迷思,得出一個二維的數字系統。
可以見到,這是一個革命性的新數字系統,有很多在一維數線上不可能的特性 - 例如正弦(sine)竟然可超過 1!虛數的應用更加進入了物理學,但不時以j代替i,以免與電流符號混淆。
圓周率 π 是圓形的周長與真徑之比,其用途及重要性不用多說。由最古老的『周三徑一』(即 φ=3)到現代準確度達百萬位的計算,關於 π 的故事幾可平行於人類歷史!令人迷惑的是,古人憑甚麼斷定圓周是 2 π r 及圓面積是 π r2?
計算π有很多方法,其中一個有趣的方法是
理論上可以由此把π計出來,但要很久很久很久...(打呵欠)。
1 當然重要,它是我們第一個學習的數字呀!其實 1 應該是最常用的數字罷。究竟「一」的概念是否在天生的,亦存在爭議。當然在哲學層面1也是重要的,有所謂『萬法歸一』嘛!
0 的重要性,亦不用多說。但 0 是甚麼,卻不好解釋。自 0 作為位置符號(例:用以區分17或107)面世,以至被接受成數字,它的歷史充滿着哲學和實用的比拼 - 畢竟把「零」、「無」、「道」、「空」四個概念混淆仍大有人在。
最後,如果閣下是在找尋『最美麗容貎的方程式』,這篇文章標題可能誤導了你,請容筆者說句「對不起」。
Saturday, February 25, 2006
對美的追求:由 φ 與 π 到電子音樂
| 右邊的希臘神殿號稱根據黃金比例,φ=1.618...所建,但實則測度卻是1.71,有接近 6% 的誤差!就統計學而言,這誤差太大了。 |  |
 右邊的大金字塔的底邊長度與高度之比乘以2是圓周率,π=3.1416...。實際測度是3.16,誤差只是 0.6% ,好像不錯;但若同時量度其他金字塔,會令人懷疑與圓周率關係完全是巧合(見這裡)。 |  |
為甚麼會有這些誤解?
首先,是對古代文明的驚歎及誤解,不自覺把現今科學知識套入古代時空中。
其次,是太強調美學與數學的關係(似乎源於文藝復興),容易以主觀願望令人接受一些較大的誤差。
在想把美學理性化的年代,這些似乎不可避免;但究竟美是否真可以純理性研究?
曾經看過一套卡通片,有一個星球科技先進,每個音符都太完美了,結果地球上一個五音不全的少女歌聲被視為驚艷!
事實上,現代的音樂軟件已可得出最完美的聲音,卻先去人性化。所以電子音樂家反而故意加上一些干擾,反而聽得舒服。某音樂人曾說:
"With modern music software it’s easy to create a perfectly even sine-wave tone. The sound will annoy you after listening to it for a few seconds.
Why is that? One of the reasons is that it is too even, too perfect. If you add a little modulation too it, the sine-wave is beginning to sound more interesting."
Friday, February 24, 2006
黃金比例
上一篇談到所謂美的面譜,φ-mask,宣稱黃金比例(φ=1.618...)是人類美的標準。但盡信書不如無書,畢竟那個卡通人面也不見得真是美!事實上,Dr. Stephen Marquardt的所謂證據其實有極大的主觀成分!

很多人說黃金比例是古希臘人對美的定義,但這純綷是誤傳。關於黃金比例的美的理論,很多時不是主觀,就是有些穿鐅附會成分。最出名是人的身高與肚臍位置高度成黃金比例〔見左圖〕,其實也沒甚科學理論支持,只是達文西的想法影嚮了後世藝術家而已!
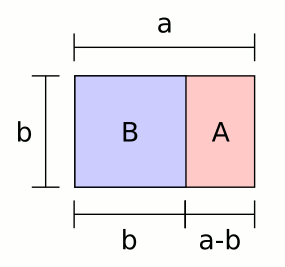
在George Markowsky的文章中揭露了很多關於黃金比例的謬誤。其中關於最美長方形的研究,發現人眼中最美的長方形,原來不是黃金比例的長方形〔見右圖 φ=1/b=b/a〕,打破了藝術家很多關於黃金比例的迷思。
有興趣的讀者,也可以看看Mario Livio的《黃金比例》(原名The Golden Ratio),前些兒商務印書店還有售。此書介紹黃金比例及有關謬誤,可以推荐給初學者。
因為黃金比例的特殊數學性質,令它在自然界及統計學有一定的地位;或者最後真的被證明是美的客觀標準,也未可知!
黃金比例其實是 φ=(√5 + 1)/2,但最有趣的表達式,是連分數如下:
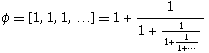

很多人說黃金比例是古希臘人對美的定義,但這純綷是誤傳。關於黃金比例的美的理論,很多時不是主觀,就是有些穿鐅附會成分。最出名是人的身高與肚臍位置高度成黃金比例〔見左圖〕,其實也沒甚科學理論支持,只是達文西的想法影嚮了後世藝術家而已!

在George Markowsky的文章中揭露了很多關於黃金比例的謬誤。其中關於最美長方形的研究,發現人眼中最美的長方形,原來不是黃金比例的長方形〔見右圖 φ=1/b=b/a〕,打破了藝術家很多關於黃金比例的迷思。
有興趣的讀者,也可以看看Mario Livio的《黃金比例》(原名The Golden Ratio),前些兒商務印書店還有售。此書介紹黃金比例及有關謬誤,可以推荐給初學者。
因為黃金比例的特殊數學性質,令它在自然界及統計學有一定的地位;或者最後真的被證明是美的客觀標準,也未可知!
黃金比例其實是 φ=(√5 + 1)/2,但最有趣的表達式,是連分數如下:
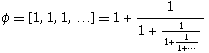
Wednesday, February 22, 2006
心善則美?平均則美!
前些時有套電視劇宣揚所謂『心善則美』,似乎太過童話化。若如是,則美容院早關門大吉,怎會成行成市!
有些人以手術追求美,即人造美女,感覺頗嚇人。但究竟誰判別怎樣變臉才是貌美?是顧客還是醫生?根據甚麼標準?若美貌標準改變了,是否要再做一次手術?
當然,關於何謂美貌,已有很多科學研究。在維基百科中關於美及吸引力的討論,學術化得令人窒息。
在2005年,有一篇關於美貌的論文《Attractiveness of own-race, other-race, and mixed-race faces》,香港報章也有提及。研究員要以統計學模形融合不同的臉孔,得出不同的虛擬容貌,然後邀請參與者把不同的臉孔按美貎程度評分。結果是相熟人士的平均面孔,是最吸引的!
也可以說,我們心中的美人兒,就是在我們「中間」!美人,原來不是如何特出,而是如何平均。
論文也說為何有這樣美的感覺:雖然生育已可能不是最要緊,但人類潛意識還是要找個基因最好的;與大多數人相同的基因,必是最好的;就這樣,多數人的平均,便成了選擇的最簡單條件!
噢!當然還有所謂黃金比例 φ=1.1618,面孔的相關部分適合黃金比例,被相信是美的條件。不信,可以自己去看看這裡。Dr. Stephen Marquardt由此而得出著名的 φ-面譜(phi mask),宣稱是美的模型,如下圖示 -
當然心善仍是美,但卻不是貌美,應該是氣質的美罷!
有些人以手術追求美,即人造美女,感覺頗嚇人。但究竟誰判別怎樣變臉才是貌美?是顧客還是醫生?根據甚麼標準?若美貌標準改變了,是否要再做一次手術?
當然,關於何謂美貌,已有很多科學研究。在維基百科中關於美及吸引力的討論,學術化得令人窒息。
在2005年,有一篇關於美貌的論文《Attractiveness of own-race, other-race, and mixed-race faces》,香港報章也有提及。研究員要以統計學模形融合不同的臉孔,得出不同的虛擬容貌,然後邀請參與者把不同的臉孔按美貎程度評分。結果是相熟人士的平均面孔,是最吸引的!
也可以說,我們心中的美人兒,就是在我們「中間」!美人,原來不是如何特出,而是如何平均。
論文也說為何有這樣美的感覺:雖然生育已可能不是最要緊,但人類潛意識還是要找個基因最好的;與大多數人相同的基因,必是最好的;就這樣,多數人的平均,便成了選擇的最簡單條件!
噢!當然還有所謂黃金比例 φ=1.1618,面孔的相關部分適合黃金比例,被相信是美的條件。不信,可以自己去看看這裡。Dr. Stephen Marquardt由此而得出著名的 φ-面譜(phi mask),宣稱是美的模型,如下圖示 -
 |  |
當然心善仍是美,但卻不是貌美,應該是氣質的美罷!
Tuesday, February 21, 2006
求存求善
Richard Dawkins的著作《The Selfish Gene》中,基因的自私引致物種的演化及社會的發展,譬如:工蟻辛勤勞動,哺育幼蟲,為的是使自己的基因延續下去。如是者,行善也是自利。
現代經濟學認為人的自利行為,是人類經濟活動的基石。如是者,自利也是行善。
或者可以簡單的說:求善就是求存。
但求甚麼的存在?求自身的存在?求家庭的存在?求國家的存在?求民族的存在?求文化的存在?求人類的存在?抑或求大自然的存在?
有謂自身存在是小我小善,其他的是相對的大我大善,所以有『犧牲小我,完成大我』之說。
若真有輪迴,大我存在,可保障小我來生的存在;小我和大我沒有根本分別。
不過有時看來的善,其實是惡;看來是惡,其實是善。限制外國貨,看來可保障本國工人,但其實損害消費者,反倒可能傷害經濟;接種牛痘,把病毒輸入身體,似乎有害,但卻可刺激免疫力,幫忙抗病。
有說『善有善報,惡有惡報』,但認稱善惡,倒未必容易。怪不得古人云『格物明德』:要知道事實的真貌,才能明辨是非。
但事實的真貌,因果的關係,當然難以掌握。要掌握善惡,還是要靠五個字:教育與研究。
現代經濟學認為人的自利行為,是人類經濟活動的基石。如是者,自利也是行善。
或者可以簡單的說:求善就是求存。
但求甚麼的存在?求自身的存在?求家庭的存在?求國家的存在?求民族的存在?求文化的存在?求人類的存在?抑或求大自然的存在?
有謂自身存在是小我小善,其他的是相對的大我大善,所以有『犧牲小我,完成大我』之說。
若真有輪迴,大我存在,可保障小我來生的存在;小我和大我沒有根本分別。
不過有時看來的善,其實是惡;看來是惡,其實是善。限制外國貨,看來可保障本國工人,但其實損害消費者,反倒可能傷害經濟;接種牛痘,把病毒輸入身體,似乎有害,但卻可刺激免疫力,幫忙抗病。
有說『善有善報,惡有惡報』,但認稱善惡,倒未必容易。怪不得古人云『格物明德』:要知道事實的真貌,才能明辨是非。
但事實的真貌,因果的關係,當然難以掌握。要掌握善惡,還是要靠五個字:教育與研究。
Monday, February 20, 2006
生之謂性
朋友的文章談到人生的開始,於是想起『人之初,性本善』。當日中文老師曾提過除了孟子性善及荀子性惡之外,還有另一人。
筆者中文修飬有限,唯有上網查詢。孟子和告子之間與荀子和孟子之間人性觀的爭論,原來一向是中國人性論史的重要課題。
網上一篇文章《告子、孟子和荀子的人性論證平議》,作者張炳陽的解釋給筆者上了一課。
告子認為人的本質(性)無所謂善與不善,所謂食色性也,道德是後天的枷鎖;告子的「善」是相對的,沒有標準的。
孟子認為人性不只食與色的動物性,還有人天生傾向善的感情,等待萠芽;孟子的「善」是「心善」,其實是指人心所向。
荀子認為人天生感情是粗糙且沒有傾向(即性本惡),需要後天教導。荀子的「善」是指「禮義法正」的行俓。
筆者不欲班門弄斧,但甚麼稱為『善』倒是個問題。文章中說三人的善根本不同。
根據現令資本主義經濟學,每個人的自私心反而推動社會進步;就如工蟻努力工作,餵哺幼蟲,其實是要令自己的基因(與幼蟻完全相同)保存下去。
如是說,為善亦只是生存必需而已!不過可能要透過教育,明白怎才可以為善,可以生存。當然受制於還境,一人的善可能是他人的惡。
如是說,告子正確,孟子似乎也對,但荀子又不大錯!
是了,所謂『有情眾生』,似乎萬物也是性本善;因為所謂狼子野心,對狼而言,亦是善!
在電視劇《覆雨翻雲》中,立志推翻明朝的大奸角,亦只是一心為同族人(蒙古人)做事的『義士』而已!
筆者中文修飬有限,唯有上網查詢。孟子和告子之間與荀子和孟子之間人性觀的爭論,原來一向是中國人性論史的重要課題。
網上一篇文章《告子、孟子和荀子的人性論證平議》,作者張炳陽的解釋給筆者上了一課。
告子認為人的本質(性)無所謂善與不善,所謂食色性也,道德是後天的枷鎖;告子的「善」是相對的,沒有標準的。
孟子認為人性不只食與色的動物性,還有人天生傾向善的感情,等待萠芽;孟子的「善」是「心善」,其實是指人心所向。
荀子認為人天生感情是粗糙且沒有傾向(即性本惡),需要後天教導。荀子的「善」是指「禮義法正」的行俓。
筆者不欲班門弄斧,但甚麼稱為『善』倒是個問題。文章中說三人的善根本不同。
根據現令資本主義經濟學,每個人的自私心反而推動社會進步;就如工蟻努力工作,餵哺幼蟲,其實是要令自己的基因(與幼蟻完全相同)保存下去。
如是說,為善亦只是生存必需而已!不過可能要透過教育,明白怎才可以為善,可以生存。當然受制於還境,一人的善可能是他人的惡。
如是說,告子正確,孟子似乎也對,但荀子又不大錯!
是了,所謂『有情眾生』,似乎萬物也是性本善;因為所謂狼子野心,對狼而言,亦是善!
在電視劇《覆雨翻雲》中,立志推翻明朝的大奸角,亦只是一心為同族人(蒙古人)做事的『義士』而已!
Friday, February 17, 2006
情由心生?心隨情動!
 |  | 心 | ♥ |
| © Kathy Mak September 2004 - 相片來源:香港中文大學 | 說文解字的「心」 | 現代中文的「心」 | 歐洲傅入的「心」形 |
當思想感覺時,就會心跳。古人斷定心是思想之源,但其實因果倒置,腦部思想需要大量血液運送飬分,以致心跳加速:-所以『情由心生』是錯,『心隨情動』才真!
但情由心生的想法,結果是「心」「忄」成為多數情感字匯的徧傍,例如「愛」、「惡」、「怨」、「恕」、「情」、「恨」、「悔」、「憎」。
中文的「心」,是象形的極致!且看《說文解字》的「心」,以致現代的「心」,都隱約見到心臟的形象。
歐洲的心形♥,相比就較簡單,但卻更容易讓人發揮創意¹。心形朱古力、心形薯仔、心形賀咭等,都是送給情人的恩物!
註1:♥是數學上所謂簡單通連的形狀,即中間沒有斷裂或空洞。
Tuesday, February 14, 2006
朱古力的學問
中國元宵之後西方情人節,就說說頗受歡迎的朱古力。
以前在《多性戀》曾介紹真菌網站在多年前二月的文章。這個網站每月都會介紹不同的真箘,而二月的往往與情人節有關。今年二月這個網站介給是有關朱古力的真菌。
首先是叢枝菌根菌(Acaulospora scrobiculata)一類與可可樹根作共生關係的真菌,幫助可可樹吸收泥土的飬分。
然後是把可可豆發酵的酵母菌,例如克魯斯假絲酵母(Candida krusei),它幫助減低可可豆的苦味。
遠在印加文化之始,印第安人開始種植可可樹,可可豆甚至能作為通用貨幣。印第安人以可可豆汁加入各種香料成為飲料,此飲法輾轉傳入歐洲;十七世紀時,糖取代胡椒成為最受歡迎的朱古力添加劑;隨着英法各國自行種植可可樹,打破西班牙襲斷,本是貴族飲料的朱古力終於進入平民百姓家。
為甚麼人會喜歡略帶的苦味朱古力?研究指出可可豆有多種刺激大腦的化合物(如㗎啡因(caffeine)及安南得邁(anandamide)),帶出歡愉的感覺。但我想商人的推銷,更是加強朱古力是甜蜜化身的地位!
朱古力是有益或有害,仍具爭議,但適可而止,永遠是最佳做法。
在《The Exploratorium》有一篇關於朱古力的特刊,值得一看。
朱古力,不知為何又叫巧克力,但我總覺前者較好,皆因大多數朱古力都是近朱色(紅色)的。
以前在《多性戀》曾介紹真菌網站在多年前二月的文章。這個網站每月都會介紹不同的真箘,而二月的往往與情人節有關。今年二月這個網站介給是有關朱古力的真菌。
首先是叢枝菌根菌(Acaulospora scrobiculata)一類與可可樹根作共生關係的真菌,幫助可可樹吸收泥土的飬分。
然後是把可可豆發酵的酵母菌,例如克魯斯假絲酵母(Candida krusei),它幫助減低可可豆的苦味。
遠在印加文化之始,印第安人開始種植可可樹,可可豆甚至能作為通用貨幣。印第安人以可可豆汁加入各種香料成為飲料,此飲法輾轉傳入歐洲;十七世紀時,糖取代胡椒成為最受歡迎的朱古力添加劑;隨着英法各國自行種植可可樹,打破西班牙襲斷,本是貴族飲料的朱古力終於進入平民百姓家。
為甚麼人會喜歡略帶的苦味朱古力?研究指出可可豆有多種刺激大腦的化合物(如㗎啡因(caffeine)及安南得邁(anandamide)),帶出歡愉的感覺。但我想商人的推銷,更是加強朱古力是甜蜜化身的地位!
朱古力是有益或有害,仍具爭議,但適可而止,永遠是最佳做法。
在《The Exploratorium》有一篇關於朱古力的特刊,值得一看。
朱古力,不知為何又叫巧克力,但我總覺前者較好,皆因大多數朱古力都是近朱色(紅色)的。
Sunday, February 12, 2006
數學燈謎
元宵佳節,讓我也來湊湊興,來個燈謎,全部射數學名詞:
1.郵費;
2.祖訓;
3.美顏大忌(諧音格);
4.搶手照相;
5.員;
6.二牛打架;
7.致病者(中英格);
8.謊話連篇(中英格)
『中英格』是我自創的名詞,指經“中文→英文→中文”的過程。
例:約會,射食品,中英格
答案:棗(解:約會→ date →棗)
以上燈謎其中除5,6外,皆是拙作,煩請賜教。
有朋友謂當中數學名詞太難,不適合作燈謎。我想同理,現今《大學》、《論語》等文章也不宜採用。
不過有時或者應弄弄花巧。怱然想起:王安石的「明月枝頭叫,黃狗臥花心。」給蘇東坡改成「明月當空照,黃狗臥花蔭。」後者似乎更言知成理。但原來王安石的「明月」是一種鳥,「黃狗」是一種蟲 - 他的詩故作玄虛卻另有一番奇趣!
不過我想沒人用明月鳥及黃狗蟲作燈謎。不知兩者的學名是甚麼?
燈謎謎底:1.函數 2.公理 3.面積(面漬) 4.映射 5.圓心 6.對頂角 7.矢量(vector) 8.李群(Lie group)
1.郵費;
2.祖訓;
3.美顏大忌(諧音格);
4.搶手照相;
5.員;
6.二牛打架;
7.致病者(中英格);
8.謊話連篇(中英格)
『中英格』是我自創的名詞,指經“中文→英文→中文”的過程。
例:約會,射食品,中英格
答案:棗(解:約會→ date →棗)
以上燈謎其中除5,6外,皆是拙作,煩請賜教。
有朋友謂當中數學名詞太難,不適合作燈謎。我想同理,現今《大學》、《論語》等文章也不宜採用。
不過有時或者應弄弄花巧。怱然想起:王安石的「明月枝頭叫,黃狗臥花心。」給蘇東坡改成「明月當空照,黃狗臥花蔭。」後者似乎更言知成理。但原來王安石的「明月」是一種鳥,「黃狗」是一種蟲 - 他的詩故作玄虛卻另有一番奇趣!
不過我想沒人用明月鳥及黃狗蟲作燈謎。不知兩者的學名是甚麼?
燈謎謎底:1.函數 2.公理 3.面積(面漬) 4.映射 5.圓心 6.對頂角 7.矢量(vector) 8.李群(Lie group)
Saturday, February 11, 2006
失敗的上一篇
上一篇其實非常失敗,剎那的衝動寫下標題。
原以為找0=1不難,怎知所想到的例子原來都是 f(1)=f(0) 的函數而已。
想勉強把『無陰功=陰功』,『好不容易=好容易』加上去,把似乎這只是『無=有』。
當然把《道德經》拉進來,可能有:0=無=道=有=1。但這似乎不太道德。
再加上www.blogger.com原來還未支援mathml,不容易輸入數學符號,更使我寫得意興蘭珊。
不過既然已開了頭,又不想放棄,最後還是把那篇不成氣候的文章發表了。
希望之後再也沒有這麼失敗之作!
---- 立此存照,以作警愓!
原以為找0=1不難,怎知所想到的例子原來都是 f(1)=f(0) 的函數而已。
想勉強把『無陰功=陰功』,『好不容易=好容易』加上去,把似乎這只是『無=有』。
當然把《道德經》拉進來,可能有:0=無=道=有=1。但這似乎不太道德。
再加上www.blogger.com原來還未支援mathml,不容易輸入數學符號,更使我寫得意興蘭珊。
不過既然已開了頭,又不想放棄,最後還是把那篇不成氣候的文章發表了。
希望之後再也沒有這麼失敗之作!
---- 立此存照,以作警愓!
Friday, February 10, 2006
無性或單性?
無性繁殖=單性繁殖?沒有雄雌的生物,是無性抑或單性?
其他“0=1”的事。
0!=1!
0 × 0 × 0 ... × 0- 0 = 1 × 1 × 1 ... × 1- 1
limx → 0+x x=limx → 1+ x x
其他“0=1”的事。
0!=1!
0 × 0 × 0 ... × 0- 0 = 1 × 1 × 1 ... × 1- 1
limx → 0+x x=limx → 1+ x x
Thursday, February 09, 2006
我的第2篇
有朋友云,《我的第一篇》並非名實不符,皆因這是今年二月的第一篇。
如是,《我的第2篇》是《跨物種婚姻》後的第2篇,也非名實不符。
『減肥茶』或『瘦身套餐』起碼可以令你的荷包減肥瘦身。
『無敵海景』往往並非說謊,只是錯别字,應該是『無滴海景』!
『天下烏鴉一樣黑』的「天下」是指「沒有白烏鴉的地方」。
『貓有九命』中的「命」可定義為一隻貓生命中九分之一的時間。
『鉛筆』起碼不是鋼筆!
『灌湯餃』不過是把最後兩字倒轉來讀,即『灌餃湯』是也。
總之,有名無實,可能只是觀點與角度而已。
如是,《我的第2篇》是《跨物種婚姻》後的第2篇,也非名實不符。
『減肥茶』或『瘦身套餐』起碼可以令你的荷包減肥瘦身。
『無敵海景』往往並非說謊,只是錯别字,應該是『無滴海景』!
『天下烏鴉一樣黑』的「天下」是指「沒有白烏鴉的地方」。
『貓有九命』中的「命」可定義為一隻貓生命中九分之一的時間。
『鉛筆』起碼不是鋼筆!
『灌湯餃』不過是把最後兩字倒轉來讀,即『灌餃湯』是也。
總之,有名無實,可能只是觀點與角度而已。
Tuesday, February 07, 2006
多性戀
有沒發覺,科幻小說中的外星人,要麼是單性(以至要研究地球人的兩性生活!),要麼也是兩性(這是和地球人發生戀愛的條件)。
為甚麼外星人不會有比地球人更複雜的愛情生活?不會有三性,四性,甚至更多?
一個可能是,科幻小說作家的想像力掌握不了多性生活!這也難怪,人是很難想像未見過的東西。
世上有否多性生物?有,但不是動物,而是真箘!據真箘專家Tom Volk在2000年情人節前後一篇關於真箘性生活的文章 http://botit.botany.wisc.edu/toms_fungi/feb2000.html 所載,世上有一種名為裂褶箘(Schizophyllum commune) 的常見真箘共有超過28000種性别!
該篇文章是為情人節所寫,正好現在拿來討論(:p)
多性真箘的性别基因都是一對兒,一記作A,一記作B。不同的A或不同的B都定義出不同的性别,如 A1B1,A1B2,A2B1,A2B2就代表不同的四種性别。兩個同類真箘要結合,就要A及B皆不同,如 A1B1與 A2B2,及 A1B2與 A2B1。
裂褶箘有300多種 A 及90多種 B,怪不得有如此多性别;而每種性别可與超過27997種其他性别結合,性生活夠多姿多采罷!
人類只有兩種性别就有這麼多事,試想像若人類有這麼多性别,是甚麼光景!?
不過我不會想這個太多了,現在要想想怎樣過情人節,嘻嘻。
為甚麼外星人不會有比地球人更複雜的愛情生活?不會有三性,四性,甚至更多?
一個可能是,科幻小說作家的想像力掌握不了多性生活!這也難怪,人是很難想像未見過的東西。
世上有否多性生物?有,但不是動物,而是真箘!據真箘專家Tom Volk在2000年情人節前後一篇關於真箘性生活的文章 http://botit.botany.wisc.edu/toms_fungi/feb2000.html 所載,世上有一種名為裂褶箘(Schizophyllum commune) 的常見真箘共有超過28000種性别!
該篇文章是為情人節所寫,正好現在拿來討論(:p)
 |
| 裂褶箘,相片來源:OSU |
多性真箘的性别基因都是一對兒,一記作A,一記作B。不同的A或不同的B都定義出不同的性别,如 A1B1,A1B2,A2B1,A2B2就代表不同的四種性别。兩個同類真箘要結合,就要A及B皆不同,如 A1B1與 A2B2,及 A1B2與 A2B1。
裂褶箘有300多種 A 及90多種 B,怪不得有如此多性别;而每種性别可與超過27997種其他性别結合,性生活夠多姿多采罷!
人類只有兩種性别就有這麼多事,試想像若人類有這麼多性别,是甚麼光景!?
不過我不會想這個太多了,現在要想想怎樣過情人節,嘻嘻。
Monday, February 06, 2006
跨物種婚姻
注意:標題是『跨物種婚姻』,不是『跨種族婚姻』。
在神話小說裡,這種事很多,但動物多要先化為人身。如《聊齋》中有人狐成婚,《白蛇傳》的白素貞(蛇妖)與許仙等。成語《南柯一夢》中淳于棼成為蟻國駙馬亦在此列。在現實中,有與生雞拜堂,但這只是以生雞作代表而已。人與獸的結合,當然被視為不道德。
在科幻小說裡,似乎所有高等生物都可以相戀、結合、生育,如《龍珠》中的地球人和撒亞人,《星空奇遇記》(Star Trek)中的地球人與克林貢人(Klingon)。可以知道,若他日真的有外星人來,與人類的生理結構差異太大,結婚生子的機會微乎其乎!
在大自然裡,不同物種幾乎都不可能結合。即使人工環境內較接近的物種能結合,生下的孩子極有可能不育,就如虎與獅所生的獅虎(虎父獅母)或虎獅(獅父虎母),及驢與馬所生的騾。這些雜種的誔生,亦被動物權益者視之為不道德。
在神話小說裡,這種事很多,但動物多要先化為人身。如《聊齋》中有人狐成婚,《白蛇傳》的白素貞(蛇妖)與許仙等。成語《南柯一夢》中淳于棼成為蟻國駙馬亦在此列。在現實中,有與生雞拜堂,但這只是以生雞作代表而已。人與獸的結合,當然被視為不道德。
在科幻小說裡,似乎所有高等生物都可以相戀、結合、生育,如《龍珠》中的地球人和撒亞人,《星空奇遇記》(Star Trek)中的地球人與克林貢人(Klingon)。可以知道,若他日真的有外星人來,與人類的生理結構差異太大,結婚生子的機會微乎其乎!
在大自然裡,不同物種幾乎都不可能結合。即使人工環境內較接近的物種能結合,生下的孩子極有可能不育,就如虎與獅所生的獅虎(虎父獅母)或虎獅(獅父虎母),及驢與馬所生的騾。這些雜種的誔生,亦被動物權益者視之為不道德。
穩定婚姻
女人甲喜歡男人乙甚於她丈夫,男人乙亦喜歡女人乙甚於他妻子,容易發生婚姻問題!
所謂預防勝於治療,婚前沒有揀錯,才是最好。
對於適婚男女比例1:1的社區,有個好辨法:「每一回,未有婚約的男人輪流向未曾拒絕過他的最心儀女子求婚 - 若女子未有婚約,就要答應;若女子有婚約,但認為男人比未婚夫要好,則可以悔婚。」(見例子)
這個是『穩定婚姻問題(stable marriage problem)』其中一個數學解,但現實那有如此兒戲;就算這方法可行,誰能保證人的喜好不會隨年月而變,婚後也可變心!
不過,這個方法主要是用於僱員與工作配對,這倒不用長相廝守。
例 子:以下社區,有男人A,B,C ,D及女人a,b,c,d。A認為 a>b>c>d,B認為 a>b>d>c,C認為 c>a>b>d,D認為 a>c>b>d;a認為 B>A>C>D,b認為 B>C>D>A,c認為 A>C>D>B,d認為A>B>D>C。(>當代表更好)
第一回:A向 a 求婚,a答應;輪到B向 a 求婚,a 認為B比A好,改與B訂婚;輪到C向 c 求婚,c答婚;最後D向 a 求婚,a拒絕。結果,A和D沒有婚約。
第二回:A向 b 求婚,b答應;輪到D向 c 求婚,c拒絕。結果,只有D沒有婚約。
第三回:D向 b 求婚,b 認為D比A好,改與D訂婚。結果,A再次沒有婚約。
第四回:A向 c 求婚,c拒絕。結果,A再次沒有婚約。
第五回:A向 d 求婚,d答應。結果是,A 配 d,B 配 a,C 配 c,D 配 b。
這樣子,文章開首的情況不會發生。
所謂預防勝於治療,婚前沒有揀錯,才是最好。
對於適婚男女比例1:1的社區,有個好辨法:「每一回,未有婚約的男人輪流向未曾拒絕過他的最心儀女子求婚 - 若女子未有婚約,就要答應;若女子有婚約,但認為男人比未婚夫要好,則可以悔婚。」(見例子)
這個是『穩定婚姻問題(stable marriage problem)』其中一個數學解,但現實那有如此兒戲;就算這方法可行,誰能保證人的喜好不會隨年月而變,婚後也可變心!
不過,這個方法主要是用於僱員與工作配對,這倒不用長相廝守。
例 子:以下社區,有男人A,B,C ,D及女人a,b,c,d。A認為 a>b>c>d,B認為 a>b>d>c,C認為 c>a>b>d,D認為 a>c>b>d;a認為 B>A>C>D,b認為 B>C>D>A,c認為 A>C>D>B,d認為A>B>D>C。(>當代表更好)
第一回:A向 a 求婚,a答應;輪到B向 a 求婚,a 認為B比A好,改與B訂婚;輪到C向 c 求婚,c答婚;最後D向 a 求婚,a拒絕。結果,A和D沒有婚約。
第二回:A向 b 求婚,b答應;輪到D向 c 求婚,c拒絕。結果,只有D沒有婚約。
第三回:D向 b 求婚,b 認為D比A好,改與D訂婚。結果,A再次沒有婚約。
第四回:A向 c 求婚,c拒絕。結果,A再次沒有婚約。
第五回:A向 d 求婚,d答應。結果是,A 配 d,B 配 a,C 配 c,D 配 b。
這樣子,文章開首的情況不會發生。
Friday, February 03, 2006
高智求愛?
數學家,邏輯學家,兼迷語大師 Raymond Smullyan 在作品 Some Interesting Memories: A Paradoxical Life 中提及追求他太太 Ilsa 的經過:
首先,向當時新相識的 Ilsa,提出簡單的要求 - 『我把預測寫在紙條上。若我猜對,妳給我一個簽名;若我猜錯,就不用給。可以嗎?』 - 這樣簡單,沒理由不答應!
然後,遞上預先準備的紙條,上寫着「妳不會給我簽名,也不會給我一個吻!」如果 Ilsa 不想送吻,會出現兩種情況 - 若她不給他簽名,根據協議,她就要給;若她給他簽名,根據協議,她不用給 - 必然出現矛盾。要沒有矛盾,Ilsa 唯有送吻!
據說當時 Ilsa 真的送吻。但當然囉,世界這麼多矛盾,多一個不算多,若 Ilsa 沒有意思,做甚麼也沒用!
給初學數理邏輯的朋友:若把 p 代表『簽名』,q 代表『送吻』,則整個命題是 (~p∧~q)↔p 等價於 q。
首先,向當時新相識的 Ilsa,提出簡單的要求 - 『我把預測寫在紙條上。若我猜對,妳給我一個簽名;若我猜錯,就不用給。可以嗎?』 - 這樣簡單,沒理由不答應!
然後,遞上預先準備的紙條,上寫着「妳不會給我簽名,也不會給我一個吻!」如果 Ilsa 不想送吻,會出現兩種情況 - 若她不給他簽名,根據協議,她就要給;若她給他簽名,根據協議,她不用給 - 必然出現矛盾。要沒有矛盾,Ilsa 唯有送吻!
據說當時 Ilsa 真的送吻。但當然囉,世界這麼多矛盾,多一個不算多,若 Ilsa 沒有意思,做甚麼也沒用!
給初學數理邏輯的朋友:若把 p 代表『簽名』,q 代表『送吻』,則整個命題是 (~p∧~q)↔p 等價於 q。
數學情歌
在2003年美國五個無聊的學生組成合唱團 The Klein Four Group,
http://www.math.northwestern.edu/~matt/kleinfour/。他們的情歌,用大量語帶相關的數學詞匯,非常有趣。他們的歌先在網上流傳,出乎意料受歡迎,並於去年十一月輯錄成唱碟。(是否想起 Kellyjackie?兩者同時紅得上 Wikipedia!)
當中較有名的歌包括 Finite Simple Group (of Order Two),中文譯名可以是
簡單的一對兒 - 誰也看得明白罷?
或
有限簡單二元群 - 這是個純數學譯名,其實就是0與1(0+0=0,0+1=1,1+0=1,1+1=0)。
歌詞中的 path, smooth, simply connected, function, forgetful,等等,全都有特別的數學意義。有評語云:不知他們唱甚麼,好像是數學,但最緊要好玩!
事實上 The Klein Four Group本身就是如下一個數學物件!(可查看Wikipedia)
http://www.math.northwestern.edu/~matt/kleinfour/。他們的情歌,用大量語帶相關的數學詞匯,非常有趣。他們的歌先在網上流傳,出乎意料受歡迎,並於去年十一月輯錄成唱碟。(是否想起 Kellyjackie?兩者同時紅得上 Wikipedia!)
當中較有名的歌包括 Finite Simple Group (of Order Two),中文譯名可以是
簡單的一對兒 - 誰也看得明白罷?
或
有限簡單二元群 - 這是個純數學譯名,其實就是0與1(0+0=0,0+1=1,1+0=1,1+1=0)。
歌詞中的 path, smooth, simply connected, function, forgetful,等等,全都有特別的數學意義。有評語云:不知他們唱甚麼,好像是數學,但最緊要好玩!
事實上 The Klein Four Group本身就是如下一個數學物件!(可查看Wikipedia)
| * | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | 1 | k | j |
| j | j | k | 1 | i |
| k | k | j | i | 1 |
Wednesday, February 01, 2006
我的第一篇
歡迎閱讀《我的第一篇》。這不是我的第一篇?啍!我喜歡改這樣名實不符的標題。
名實不符的稱謂很多:
『第一屆立法會』,其實是第二屆立法會,但因政治故意把第一屆喚作臨時立法會。
『都會駅』,不是在日本的車站,其實是在香港的樓盤。
『星洲炒米』,『楊州炒飯』,及『french fries(薯條)』的地名,都不是真正的原產地,純是標搒外來貨而已!
『臨時房屋區』,臨時了超過十年。『地下鐵路』原先真的全在地下。沙田的『海旁道』,在海邊嗎?
魚,在古代泛指一切海中生物,但在現代生物學中卻有特殊定義,是以『鯨魚』,『星魚』,『八爪魚』等,在今天變得名實不符。同理還有不是樹的『香蕉樹』及『鐵樹』。
當然還有不是鉛做的『鉛筆』,有花的『無花果』,及沒有錫的『錫紙』。
名實不符的稱謂很多:
『第一屆立法會』,其實是第二屆立法會,但因政治故意把第一屆喚作臨時立法會。
『都會駅』,不是在日本的車站,其實是在香港的樓盤。
『星洲炒米』,『楊州炒飯』,及『french fries(薯條)』的地名,都不是真正的原產地,純是標搒外來貨而已!
『臨時房屋區』,臨時了超過十年。『地下鐵路』原先真的全在地下。沙田的『海旁道』,在海邊嗎?
魚,在古代泛指一切海中生物,但在現代生物學中卻有特殊定義,是以『鯨魚』,『星魚』,『八爪魚』等,在今天變得名實不符。同理還有不是樹的『香蕉樹』及『鐵樹』。
當然還有不是鉛做的『鉛筆』,有花的『無花果』,及沒有錫的『錫紙』。
Tuesday, January 31, 2006
中文及英文的性
知不知在學術文獻中『性』最常用的英文譯名之甚麼?
“sex”?錯了!是“bility”!例如『可行性』workability,『可除性』divibility,『可靠性』reliability,『可積性』integrability,『靈活性』flexibility,及『相容性』compatibility。
中國大陸自從改革開放以來,性開放的情度確實令人咋舌。大陸同胞非常接受一次性行為,例如『一次性相機』,『一次性筷子』,『一次性碗』等;相反港台人士卻極為保守,我們用『即棄相機』,『即棄筷子』,『用完即棄碗』。
很多時候,大陸人亦有意無意間加入性文字。例如『學術文章』寫成『學術性文章』,『突破發展』寫成『突破性發展』,『安全問題』寫成『安全性問題』等。
當然,對推動性開放,中國共產黨自是功不可沒。若我們搜尋大陸『性教育』網站,可知共產黨員要不斷接受『先進性教育』呢!
“sex”?錯了!是“bility”!例如『可行性』workability,『可除性』divibility,『可靠性』reliability,『可積性』integrability,『靈活性』flexibility,及『相容性』compatibility。
中國大陸自從改革開放以來,性開放的情度確實令人咋舌。大陸同胞非常接受一次性行為,例如『一次性相機』,『一次性筷子』,『一次性碗』等;相反港台人士卻極為保守,我們用『即棄相機』,『即棄筷子』,『用完即棄碗』。
很多時候,大陸人亦有意無意間加入性文字。例如『學術文章』寫成『學術性文章』,『突破發展』寫成『突破性發展』,『安全問題』寫成『安全性問題』等。
當然,對推動性開放,中國共產黨自是功不可沒。若我們搜尋大陸『性教育』網站,可知共產黨員要不斷接受『先進性教育』呢!
Monday, January 30, 2006
不純潔的數學
數學和性有啥關係?正經的,有生物學與性有關的數學模型;不大正經的,前年有人出了本名叫Mathematics and Sex的書;但更要命的,是Richard A.Gibbs在1983年刋登的一篇文章,題目是Impure Mathematics。
這文章的內容很簡單:某天一個少女不聽從媽媽吩咐,不設防地單獨走進樹林,在迷路時慘被色狼遽着,後來大了肚子,在醫院誔下孩子。
文 章中的文字完全是諧音或語帶相關的數學詞匯。例如 convergent(收歛)代替 virgin(處女),integration(積分)又解『結合』代表『交合』,significant places(有效數位)又可解『要緊部位』,L'hopital(大數學家)代替 hospital(醫院)。能夠看得明,而又笑得出的(或駡得出的),必有一定的數學修飬。
可惜的是,這是一篇以文字為中心的笑話,根本不可能翻譯成中文。
唯 一可以說的,是文章的教訓:若要保特表達式(女兒)為收歛(處女),不能讓她有一點的自由¹。(If you want to keep your expressions convergent, never allow them a single degree of freedom.)
註1:『自由』也是數學慨念。
這文章的內容很簡單:某天一個少女不聽從媽媽吩咐,不設防地單獨走進樹林,在迷路時慘被色狼遽着,後來大了肚子,在醫院誔下孩子。
文 章中的文字完全是諧音或語帶相關的數學詞匯。例如 convergent(收歛)代替 virgin(處女),integration(積分)又解『結合』代表『交合』,significant places(有效數位)又可解『要緊部位』,L'hopital(大數學家)代替 hospital(醫院)。能夠看得明,而又笑得出的(或駡得出的),必有一定的數學修飬。
可惜的是,這是一篇以文字為中心的笑話,根本不可能翻譯成中文。
唯 一可以說的,是文章的教訓:若要保特表達式(女兒)為收歛(處女),不能讓她有一點的自由¹。(If you want to keep your expressions convergent, never allow them a single degree of freedom.)
註1:『自由』也是數學慨念。
Sunday, January 29, 2006
我的第0篇
初到 blog 境,一切由零開始,這是我這篇文章標題的來由。
一些書本,可能有第0章,來放置介乎前言與正式內容之間的說話。
一些朝代,第1個皇帝會追封先父為皇,這不就是第0個皇帝?好像曹操是魏國第0個皇帝。
一些機構,它可能有個古怪的前身,如香港特區成立之初的臨時立法局,是個不是立法局的立法局,可說是第0屆立法局。
一些電腦話言,因為記憶體的初始狀態由0000(二進制的0)開始,於是所有排列(array)由0開始。
最早把0放在1之前,是甚麼人呢?
穿鑒附會的說,應是三千年前道德經的『道生一,一生二,二生三』。若我們把『道』等同『無』,把『無』量化為『0』,遂符合老袓宗第一的中華民族精神。
印度人於二千多年前發明0,但依然由1開始數。
真正的答案,是稍後的瑪雅文明,他們有傳說中的第0天,在公元前3114年8月13日。
歐洲數學家嘛,把數字由小排到大應是最自然的事,但也要在一千年前才把0納入數學體系!
一些書本,可能有第0章,來放置介乎前言與正式內容之間的說話。
一些朝代,第1個皇帝會追封先父為皇,這不就是第0個皇帝?好像曹操是魏國第0個皇帝。
一些機構,它可能有個古怪的前身,如香港特區成立之初的臨時立法局,是個不是立法局的立法局,可說是第0屆立法局。
一些電腦話言,因為記憶體的初始狀態由0000(二進制的0)開始,於是所有排列(array)由0開始。
最早把0放在1之前,是甚麼人呢?
穿鑒附會的說,應是三千年前道德經的『道生一,一生二,二生三』。若我們把『道』等同『無』,把『無』量化為『0』,遂符合老袓宗第一的中華民族精神。
印度人於二千多年前發明0,但依然由1開始數。
真正的答案,是稍後的瑪雅文明,他們有傳說中的第0天,在公元前3114年8月13日。
歐洲數學家嘛,把數字由小排到大應是最自然的事,但也要在一千年前才把0納入數學體系!
Subscribe to:
Comments (Atom)



