萬『數』皆『集』

道家曰：萬物為一。
佛家曰：萬法皆空。

數學家曰：萬數皆集！

道家及佛家的說法是以形而上學解答問題；數學家剛好相反，是希望避免形而上學。

在文明之初：數目生於實用，圖形始於美學；

隨時間演進：建築、天文、農耕、稅收等，產生新的數學，亦把各種數學枝派連繫起來；

宗教的數學：由天文與占卜，把數學引入宗教內；古希臘人，古印度教，古馬雅，以及易經等，都把數學賦與一定的神秘地位；

科技的發展：經濟及科技的火速發展，令數學的重要性大大增加，亦令『數學是甚麼？』的問題愈趨迷惑。而各種數學枝派，卻未能有效的連繫，冀望有一套共同的數學語言。　

集合，是數學家康托爾為研究無限所創造的概念。簡單來說，一個集合就是一堆東西。小學生也懂的温氏圖（見下圖），就是集合的最簡單表逹法。



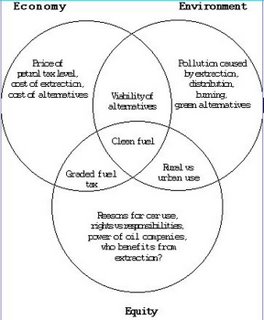
集合所載的，不用是實物：可以是一個個的數字，可以是一種種的思想，可以是一層層的概念。

慢慢地，數學家把幾乎所有的抽象數學物件，變成了一個個的集合。譬如上一篇《零與空》，便提到０是一個甚麼都沒有的集合。集合論的語言，逐步成為所有數學的共同語言。

『數學是甚麼？』在很多時候，都可變成『集合是甚麼？』。集合，就是一堆東西，看來是個非常堅實而簡明的概念，而絕大多數數學家，都可以安安樂樂的，不需要再考慮形而上學的問題。

但危險卻出現，這就是羅素悖論，最形象化的是如下問題：一個「要給所有不自已理髮的人理髮，不給任何自己理髮的人理髮」的理髮師，會不會為自己理髮？

這個例子，生動的說明不是所有的條件都可以運用；對數學來說，即不是隨便把東西放在一起，邏輯上就可以行得通。

二十世紀初的殺着，就是公理化　－　所有數學定理，由最基本的數條『公理』（即可行假設）經邏輯推論而來。於是數學變成了純粹的推理遊戲，杜絕了除便給與條件的運用問題；同時解決『集合是甚麼？』，答案是一些符號而已！

對於最深入的哲理問題，當然仍有哲學家及基礎數學家在努力鑽研（他們認為集合論仍有一些缺點，需要替代或改良）。但『萬數皆集』已是目前最一般的共識！