Discover Magazine 有篇"科學家仍困惑於人類乳房的演化"(Scientists Still Stumped By The Evolution of Human Breasts - The Crux)
內容其實了無新意, 說的就是為何女人的乳房全天候堅挺, 不似其他靈長類動物. 來來去去的就是說是因為人類能全年發情, 又或是作為備用脂肪能量儲備. 反正沒有啥可能驗證真正答案, 自然永遠停留在困惑層面呀!
(有學生問我點解冇寫嘢, 咁就寫下囉....)
數理情色
甚麼是『數理情色』?這是個以輕鬆手法討論科學知識的blog,當然也是吸引人來看我的blog的綽頭名稱!
Thursday, March 07, 2019
Friday, December 21, 2018
數學的迷人曲線
唔轉發對唔對我個Blog嘅title.
驚覺數學有多美!浪費才能「歐派函數」連日本東大生都著迷 | 鍵盤大檸檬 | ETtoday新聞雲
日本多間大學理工科的數學愛好者,組成「歐派函數熱情注入委員會」,研究函數之美,以下是其中一間大學的作品:
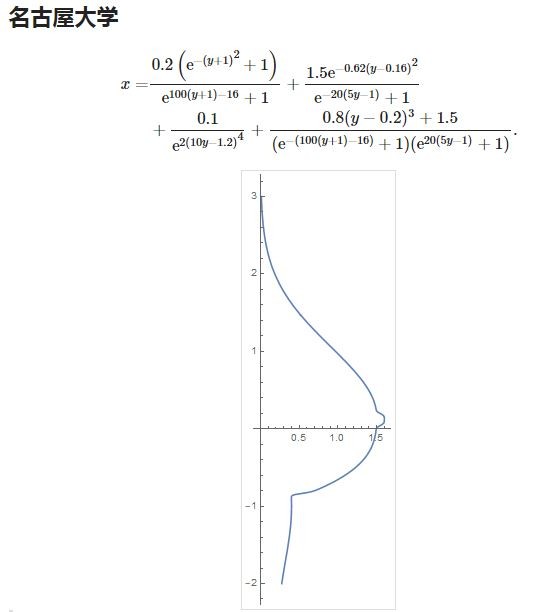
驚覺數學有多美!浪費才能「歐派函數」連日本東大生都著迷 | 鍵盤大檸檬 | ETtoday新聞雲
日本多間大學理工科的數學愛好者,組成「歐派函數熱情注入委員會」,研究函數之美,以下是其中一間大學的作品:

Friday, May 18, 2018
為何3×2=2×3? (再續)
如果有兩種不同定義的運算, 給發現如來得出相同結果, 數學家就會把兩者看作一樣.
換句話說, 假設一開始時數學家定義了兩種乘法:
m x n = m+...+m (n 個)
m * n = n+...+n (m 個)
接着數學家知道了 mxn=m*n, 他們就會毫不猶疑也接受 m x n = n+...+n (m 個)
換句說話, 除了開頭不知兩者相等的情況, 其他時候數學家會隨便使用兩個定義.
唯一例外情況, 是出習作時, 會故意強迫學生使用其中一個定義, 以強化他們的邏輯思維.
例如: 從(課本上的)定義出發, 證明2 × 3 = 3 + 3.
正確答案: 從定義出發, 2 × 3 = 2 + 2 + 2=6, 而 3+3=6, 所以2 × 3 = 3 + 3.
這裡, 我們不能直接寫 2 × 3 = 6, 而一定要寫 2 × 3 = 2 + 2 + 2=6, 皆因我們要從定義出發.
能力稍遜的學生, 通常不喜歡這類題目, 因為由定義出發, 通常較煩且少了很多可用的工具.
在數學發展史上, 若有兩個看似不同的概念, 給證明了是同一回事, 必定是一件大新聞. 因為本來的兩個概念, 都各自有不同的思考方法及數學工具. 兩者結合, 就多了很多思考方法及工具可用, 會造成數學的一次大躍進.
換句話說, 假設一開始時數學家定義了兩種乘法:
m x n = m+...+m (n 個)
m * n = n+...+n (m 個)
接着數學家知道了 mxn=m*n, 他們就會毫不猶疑也接受 m x n = n+...+n (m 個)
換句說話, 除了開頭不知兩者相等的情況, 其他時候數學家會隨便使用兩個定義.
唯一例外情況, 是出習作時, 會故意強迫學生使用其中一個定義, 以強化他們的邏輯思維.
例如: 從(課本上的)定義出發, 證明2 × 3 = 3 + 3.
正確答案: 從定義出發, 2 × 3 = 2 + 2 + 2=6, 而 3+3=6, 所以2 × 3 = 3 + 3.
這裡, 我們不能直接寫 2 × 3 = 6, 而一定要寫 2 × 3 = 2 + 2 + 2=6, 皆因我們要從定義出發.
能力稍遜的學生, 通常不喜歡這類題目, 因為由定義出發, 通常較煩且少了很多可用的工具.
在數學發展史上, 若有兩個看似不同的概念, 給證明了是同一回事, 必定是一件大新聞. 因為本來的兩個概念, 都各自有不同的思考方法及數學工具. 兩者結合, 就多了很多思考方法及工具可用, 會造成數學的一次大躍進.
Thursday, May 17, 2018
為何3×2=2×3? (續)
朋友在談論3×2=2×3時,指出小學老師提及
2 × 3 = 2 + 2 + 2
3 × 2 = 3 + 3
兩者雖然相等, 但概念不同.
這個可以帶出很多話題, 不過我想最多人注意的是:
如果有個小學生寫2 × 3 = 3 + 3算唔算錯?
注意, 我強調小學生. 因為過了小學, 再沒有人理會這件事.
我的答案是: 不清楚.
原因是"="本身有不同的意思.
"A=3" 的第一個意思是"把A的數值設為3", 第二個意思是"經過計算, 發現A的數值是3".
"f(x)=x+4" 的第一個意思是"把f(x)定義為x+4", 第二個意思是"經過計算, 發現f(x)的值是x+4".
有些人為了分開兩種意思, 故意用不同的符號. 例如用":="代表定義, "="是原本第二個的意思.
換句話說, 如果教科書上寫"m × n:=m+m+...m (n 個 m)", 則"2 × 3 := 3 + 3"是錯, 而"2 × 3 = 3 + 3"是對的.
不過, 小學課本基本上沒有區分"="的兩個意思, 所以嘛......
2 × 3 = 2 + 2 + 2
3 × 2 = 3 + 3
兩者雖然相等, 但概念不同.
這個可以帶出很多話題, 不過我想最多人注意的是:
如果有個小學生寫2 × 3 = 3 + 3算唔算錯?
注意, 我強調小學生. 因為過了小學, 再沒有人理會這件事.
我的答案是: 不清楚.
原因是"="本身有不同的意思.
"A=3" 的第一個意思是"把A的數值設為3", 第二個意思是"經過計算, 發現A的數值是3".
"f(x)=x+4" 的第一個意思是"把f(x)定義為x+4", 第二個意思是"經過計算, 發現f(x)的值是x+4".
有些人為了分開兩種意思, 故意用不同的符號. 例如用":="代表定義, "="是原本第二個的意思.
換句話說, 如果教科書上寫"m × n:=m+m+...m (n 個 m)", 則"2 × 3 := 3 + 3"是錯, 而"2 × 3 = 3 + 3"是對的.
不過, 小學課本基本上沒有區分"="的兩個意思, 所以嘛......
為何3×2=2×3?
近日, 有朋友在網上談及"為何3×2=2×3?" 令我想起一個舊笑話:
老師: 為何3×2=2×3?
學生: 因為都是6.
老師: 錯!
學生: 因為乘法符合交換律.
老師: 對了!
當然, 學生第一個答案沒錯, 第二個答案反而不自然. 就讓我來說一說.
先來一個日常生活的例子
甲是乙的生母的定義是甲是把乙生下來的女人.
請看如下兩句:
讓我們入數學正題
×符合交換律的定義是對所有數字a及b, 都有a×b=b×a.
請看如下兩句:
好了, 讓我們看看
問: 為何2×3=3×2?
答: 因為乘法符合交換律, 所以2×3=3×2.
邏輯正確, 但明明2×3=3×2是交換律的其中一個條件, 這樣寫法有點倒果為因.
問: 為何2×3=3×2?
答: 因為2×3=6及3×2=6, 所以2×3=3×2.
清楚, 明白, 簡單, 直接, 自然!
那麼, 何時才用交換律呢? 就在不要嘗試計算乘積的時候!
問: 為何x2y=yx2?
答: 因為乘法符合交換律, 所以x2y=yx2.
我們x,y可以是任何數, 我們沒法驗證所有情況, 所以用到交換律.
問: 為何1532657883×89234927498274=89234927498274×1532657883?
答: 因為乘法符合交換律, 所以1532657883×89234927498274=89234927498274×1532657883.
我這個覺得可以接受, 因為我不願意花時間把乘積計算出來.
老師: 為何3×2=2×3?
學生: 因為都是6.
老師: 錯!
學生: 因為乘法符合交換律.
老師: 對了!
當然, 學生第一個答案沒錯, 第二個答案反而不自然. 就讓我來說一說.
先來一個日常生活的例子
甲是乙的生母的定義是甲是把乙生下來的女人.
請看如下兩句:
- 因為沈殿霞生下了鄭欣宜, 所以沈殿霞是鄭欣宜的生母.
- 因為沈殿霞是鄭欣宜的生母, 所以沈殿霞生下了鄭欣宜.
讓我們入數學正題
×符合交換律的定義是對所有數字a及b, 都有a×b=b×a.
請看如下兩句:
- 因為對所有數字a及b, 都有a×b=b×a, 所以乘法符合交換律.
- 因為乘法符合交換律, 所以對所有數字a及b, 都有a×b=b×a.
好了, 讓我們看看
問: 為何2×3=3×2?
答: 因為乘法符合交換律, 所以2×3=3×2.
邏輯正確, 但明明2×3=3×2是交換律的其中一個條件, 這樣寫法有點倒果為因.
問: 為何2×3=3×2?
答: 因為2×3=6及3×2=6, 所以2×3=3×2.
清楚, 明白, 簡單, 直接, 自然!
那麼, 何時才用交換律呢? 就在不要嘗試計算乘積的時候!
問: 為何x2y=yx2?
答: 因為乘法符合交換律, 所以x2y=yx2.
我們x,y可以是任何數, 我們沒法驗證所有情況, 所以用到交換律.
問: 為何1532657883×89234927498274=89234927498274×1532657883?
答: 因為乘法符合交換律, 所以1532657883×89234927498274=89234927498274×1532657883.
我這個覺得可以接受, 因為我不願意花時間把乘積計算出來.
Friday, September 01, 2017
The Star Thrower and Nature's Way
A friend has discussed the famous The Starfish Thrower story on Facebook. This story has moved thousands of people.
I want to show him an interesting sort-of-related story which I read the Chinese translation a long time ago. As my friend does not read Chinese, I try to search for the original English version. It turns out that the Chinese translation is very famous, it is used as a Chinese textbook article in mainland China, but the original English is hard to find online. It turns out that many Chinese students have searched for it but failed. As a result, they even question the authenticity of the article.
It seems to be a New York Times article Humans, All Too Human by Michael Blumenthal on 23 July 1989. The only English website I found related to it is a response posted on New York Times one month later. Then there is a condensed version titled Nature's Way in 1990, which I can found only on Chinese websites.
I want to show him an interesting sort-of-related story which I read the Chinese translation a long time ago. As my friend does not read Chinese, I try to search for the original English version. It turns out that the Chinese translation is very famous, it is used as a Chinese textbook article in mainland China, but the original English is hard to find online. It turns out that many Chinese students have searched for it but failed. As a result, they even question the authenticity of the article.
It seems to be a New York Times article Humans, All Too Human by Michael Blumenthal on 23 July 1989. The only English website I found related to it is a response posted on New York Times one month later. Then there is a condensed version titled Nature's Way in 1990, which I can found only on Chinese websites.
If you are interested, you can find the original version and the Chinese version of Nature's Way, and the frustrations of Chinese students on this website.
What is Nature's Way about? It is a story that several men interwind with nature to save a baby turtle, which in turns led to the death of many baby turtles.
The Starfish Thrower literally tells about saving one starfish to make a difference, Nature's Way reminds us that we have to be careful such that our good deed may not be a wishy-washy thinking.
What is Nature's Way about? It is a story that several men interwind with nature to save a baby turtle, which in turns led to the death of many baby turtles.
The Starfish Thrower literally tells about saving one starfish to make a difference, Nature's Way reminds us that we have to be careful such that our good deed may not be a wishy-washy thinking.
Wednesday, June 28, 2017
一篇關於June Huh文章的讀後感
The quanta Magazine今期有篇A Path Less Taken to the Peak of the Math World是關於一位名叫June Huh 的數學家。這是一篇高水準的文章,足以讓我這個喜歡過分解讀的人,有一籃子的感想。
文章大意如下:
「June Huh在美國出生,兩歲時隨父母返回韓國生活。
在小學時一次數學成績不好,令June Huh自覺不是數學料子。他立志成為詩人,認為詩詞對現實的描繪,勝過無謂的邏輯遊戲。
他在中學時寫了很多詩,但從未發表過。事實上,他認清了現實,詩人不能糊口,所以把志向改成科普記者。結果,他進入Seoul National University時選擇了天文物理。
在大學最後一年,一位Fields Medal得奬人 Heisuke Hironaka到Seoul National University訪問,教授一年代數幾何的特別課。June Huh上了那一門課,並希望Heisuke Hironaka是他作為科普記者的第一個受訪者。
特別課很難,很多數學本科生聽不懂,退出了。June Huh也聽不懂,但既然立志做科普記者,只要稍稍明白概念就足夠。他沒退出,甚至主動接觸Heisuke Hironaka。
結果,Heisuke Hironaka看到June Huh的數學天賦,亦成為了他的數學碩士導師。
在Heisuke Hironaka的鼓勵下,June Huh報讀美國的博士課程。但因為不是數學本科生,成績也不算出眾,即使有如此著名的碩士導師撑腰,亦只是the University of Illinois(Urbana-Champaign)接受他的申請。
在唸博士的第一年,June Huh一鳴驚人,他用代數幾何的方法,解決了一個著名組合數學猜想Rota Conjecture的一個特例!
接下來,就是一個數學天才的故事,他與另外兩位天才Eric Katz及Karim Adiprasito合力解決了Rota Conjecture,現在被視為有力問鼎下屆或再下一屆的Fields Medal。順帶一提,Fields Medal只頒發給四十歲以下的數學家。」
讀後感
他小時候立志成為詩人,學人寫詩,卻沒有發表,最後放棄。感覺上不是真的因為詩人不能糊口而放棄,而是長大了發覺以前寫的只是少年強說愁的幼稚詩,不能入大雅之堂,明白不是詩人料子!
他自以為不是數學料子。事實上,他是數學料子,但不是數學考試料子。這種人,給他足夠時間,多難的數學考題都答到滿分,但只給他兩三小時,他便很吃力。他是幸運的,遇到伯樂,大多數同類都給無可奈何的考試抺殺了。
其實,他的數學成績,一直不算差,否則怎可能入讀天文物理!天文物理的數學,可不是說笑的。
在撮要中,只有一句"他用代數幾何的方法,解決了一個著名組合數學猜想Rota Conjecture的一個特例",但其實在文章中,這段文章佔有三分之一。因為,這反映了他的天才與及影响。
所謂隔行如隔山,即使是不同的數學分枝,他們的思考方法及通用語言,都有分別。把兩個數學分枝連起上來,難度非常大,而一旦成功,就會給後來的數學家更多有用的功具。
坐標幾何利用算術來研究幾何,萬有引力理論把天上及地上的現象連在一起,電磁學把電與磁合一。博奕論成為生物學與經濟學的基礎工具。可以說,中國文人口中不清不楚的萬法歸一,正在由科學家一點一滴的完成。
作為天才,他是有一點與別不同。其他天才要麼是數學神童,要麼大學時已鋒忘畢露,好像他大學畢業才半途出家做數學,又真是異數。
文章大意如下:
「June Huh在美國出生,兩歲時隨父母返回韓國生活。
在小學時一次數學成績不好,令June Huh自覺不是數學料子。他立志成為詩人,認為詩詞對現實的描繪,勝過無謂的邏輯遊戲。
他在中學時寫了很多詩,但從未發表過。事實上,他認清了現實,詩人不能糊口,所以把志向改成科普記者。結果,他進入Seoul National University時選擇了天文物理。
在大學最後一年,一位Fields Medal得奬人 Heisuke Hironaka到Seoul National University訪問,教授一年代數幾何的特別課。June Huh上了那一門課,並希望Heisuke Hironaka是他作為科普記者的第一個受訪者。
特別課很難,很多數學本科生聽不懂,退出了。June Huh也聽不懂,但既然立志做科普記者,只要稍稍明白概念就足夠。他沒退出,甚至主動接觸Heisuke Hironaka。
結果,Heisuke Hironaka看到June Huh的數學天賦,亦成為了他的數學碩士導師。
在Heisuke Hironaka的鼓勵下,June Huh報讀美國的博士課程。但因為不是數學本科生,成績也不算出眾,即使有如此著名的碩士導師撑腰,亦只是the University of Illinois(Urbana-Champaign)接受他的申請。
在唸博士的第一年,June Huh一鳴驚人,他用代數幾何的方法,解決了一個著名組合數學猜想Rota Conjecture的一個特例!
接下來,就是一個數學天才的故事,他與另外兩位天才Eric Katz及Karim Adiprasito合力解決了Rota Conjecture,現在被視為有力問鼎下屆或再下一屆的Fields Medal。順帶一提,Fields Medal只頒發給四十歲以下的數學家。」
讀後感
他小時候立志成為詩人,學人寫詩,卻沒有發表,最後放棄。感覺上不是真的因為詩人不能糊口而放棄,而是長大了發覺以前寫的只是少年強說愁的幼稚詩,不能入大雅之堂,明白不是詩人料子!
他自以為不是數學料子。事實上,他是數學料子,但不是數學考試料子。這種人,給他足夠時間,多難的數學考題都答到滿分,但只給他兩三小時,他便很吃力。他是幸運的,遇到伯樂,大多數同類都給無可奈何的考試抺殺了。
其實,他的數學成績,一直不算差,否則怎可能入讀天文物理!天文物理的數學,可不是說笑的。
在撮要中,只有一句"他用代數幾何的方法,解決了一個著名組合數學猜想Rota Conjecture的一個特例",但其實在文章中,這段文章佔有三分之一。因為,這反映了他的天才與及影响。
所謂隔行如隔山,即使是不同的數學分枝,他們的思考方法及通用語言,都有分別。把兩個數學分枝連起上來,難度非常大,而一旦成功,就會給後來的數學家更多有用的功具。
坐標幾何利用算術來研究幾何,萬有引力理論把天上及地上的現象連在一起,電磁學把電與磁合一。博奕論成為生物學與經濟學的基礎工具。可以說,中國文人口中不清不楚的萬法歸一,正在由科學家一點一滴的完成。
作為天才,他是有一點與別不同。其他天才要麼是數學神童,要麼大學時已鋒忘畢露,好像他大學畢業才半途出家做數學,又真是異數。
Thursday, July 07, 2016
試譯Scott Aaronson的《數造傳奇》影評
“Largely just men doing sums”: My review of the excellent Ramanujan film
[警告:內有劇透,以及連分數算式.]
這陣子,我和太太忙於照顧小孩,很難得有機會去看《數造傳奇The Man Who Knew Infinity》首映(鳴!他好幸褔呀!我太太不肯陪我看首映!)—此片是關於印度數學家拉馬努金 Srinivasa Ramanujan與英國數學大師哈代G. H. Hardy的亦師亦友關係。此放映會之後,還可以與該片的導演Matthew Brown, 該片的藍本傳記作家Robert Kanigel ,及該片的顧問費爾茲獎得主Manjul Bhargava面談。
我是在90年代初期拜讀Kanigel所著The Man Who Knew Infinity,對我影响甚深。過千頁的傳記談及拉馬努金謎樣的思考方法,他與哈代及Littlewood的關係,他對數學分析的影响。當然書中也有對當年13歳的書蟲極為震撼的算式:例如
拜讀此書後數年,我在加拿大遇到過真正認識哈代的數學大師Richard K. Guy, 我的中學同學沒有一個知道哈代嘛!(我在卡加里大學時也和Guy說過話呢!)除為甚麼我這麼興奮,因為我對所有數學家的電影及傳記都很感興趣。
閒話說完,《數造傳奇》究竟如何?當然不可能滿分喲!但這肯定是到目前為止,最好最接近史實的數學家電影。趁未落畫,好去睇啦!
讓我先從數學講起。
在電影開場時,便很貼題的以拉馬努金的筆記作為背景。在片中的後半段,很正確地解釋了拉馬努金與Hardy最令人稱為的成果,就是發現了
讓我先從數學講起。
在電影開場時,便很貼題的以拉馬努金的筆記作為背景。在片中的後半段,很正確地解釋了拉馬努金與Hardy最令人稱為的成果,就是發現了
及給出正確證明。
電影很清楚的說明,數學家醉心的並不是數學的應用,而是數學的美。虔試的拉馬努金認為他是在寫下女神的旨意,而無神論者哈代亦以數學作為他的心靈歸宿。
關於數學的正確性,未受過正規訓練拉馬努金很信任直觀,而哈代則強調證明,因而產生了張力。片中對兩者的描述都頗中肯。不似荷理活電影老是貶低嚴謹思維的重要性。
不過,對於數學愛好者來說,片中對數學的描述還未足夠。
接着,讓我談談電影的其他支節。
有人不滿演員太老。當年哈地不過四十,Jeremy Irons來演老了三十年。拉馬努金的妻子Janaki結婚時只有九歳(!),丈夫去英國時只是十四,卻找個成熟的Devika Bhise來演。(如果要找個年紀相乎的演員,我突然想起黑白片時代的馮寶寶!)此外 J. E. Littlewood 由一個感覺似諧星的演員來做,很難令人感到他也是一代的數學大師。
在片中,對數學邏輯有傑出貢獻的哲學家Bertrand Russell,只是個過場角色。雖則現實裡他與哈代是好朋友兼同時是第一次大戰的和平主義者,但哈代向他請教如何幫助拉馬努金,應是子虛烏有。
其實這些都不重要。最令我介懷的,是片中誇大了的種族岐視。有個數學教授感到拉馬努金侮辱而趕了他出課室?拉馬努金被英國士兵拳打腳踢?哈代見到他的傷勢不聞不問?是的,拉馬努金會受岐視及感到寂寞,但劍橋社會不見得會如此赤裸裸。電影選擇直接見得到的傷害,避開難拍的隱藏岐視,反而減弱它的吸引力。
還有,電影如實的拍出劍橋三一書院變成戰地醫院及學生操兵出陣,但要拉馬努金親眼見到屍體?不用罷,現實經已很殘酷。
電影似乎引導觀眾接馬努金是死於肺癆。但近年有研究顯示,他是死於由印度帶過去的阿米巴病—這是一種當年很難確診但醫很好的病。片中沒有講到拉馬努金在回去印度的那一年,其實不斷與哈地書信往來,直到病殁。很多人認同這抺去這一年是好的選擇,但若然是我,我會拍出來!
夠了!以荷里活電影的角度,以上的批評已是吹毛求疵。要記住,Brown用了近十年來尋找資金,來拍這套電影;他本來可以早些籌到金錢,但他拒住加插拉馬努金與由英國女星主演的白人護士熱戀的吸金情節!可以想像,加插P(n)解釋時的一番鬥爭。
看着一大堆公式,不會讓你興奮。以感情為主題,你很難說不喜歡,但它就是枯燥。拍出水準,但它其實只是一班男人在計數。這些算式很重要,但直至最後一幕談及黑洞,觀眾是不能領略它對科學發展有多重要。
Subscribe to:
Posts (Atom)