社會“科學”？

教育學、經濟學、政治學，都屬於社會學範籌，擁有同一特點：實驗難！

準確點說，是控制實驗難。為甚麼呢？

首先，一些實驗的道德問題太大－－舉例說，有理論說如何如何一個人會破產，或如何如何一個人會變成罪犯，可以做實驗證明嗎？相反，有理論說如何如何一間公司會發展得更好，或如何如何一個兒童會成長得更好，有多少老闆或家長會冒着理論錯誤的風險做實驗？

其次，一個完美的科學實驗，要令得變數愈少愈好－－例如要知道重量及壓力的關係，就要保持溫度不變，以免把問題複雜化。但與人有關的事，這可以做到嗎？

最後，變數太多－－即使結果與實驗不同，也難知是理論錯，還是其他環節出錯！人往往是頑固的，不承認是理論錯，並諉過於其他。這導致理論發展的困難。

第三點，其實才是最致命的弱點。現代科學家多根據卡爾·波普爾（Karl Popper）的說法，認為只有一個理論是可偽證的，即有機會被證明是錯的，才算是科學（science）！

占卜、氣功、風水，相關的專家往往不肯「認低威」－－這也難怪，理論錯誤會丟飯碗－－所以很難成為被接受的科學。

有很多宗教信徒，常說自己的宗教是科學，卻其實犯了兩個錯誤：一個大錯，及一個極大錯。

大錯是宗教不可能偽證，諸如不可能用實驗測試神是否存在，所以不是科學－－但這只是與現代科學定義相悖而已。

極大錯是把宗教置於科學之下！科學是希望用『理論模型』以解釋自然現象，而可偽證表明這未必是絕對的。所以稱宗教為科學根本不能證明宗教的正確性！宗教之所以稱為信仰，是以『信心』為主，不應該要證明！

若然相信科學，應該把科學包含於宗教之內，而不是倒轉。我們可以說「科學是回教」，「科學是佛教」，但絕不可說「回教是科學」，「佛教是科學」！

互聯網的出現，給社會學一個做實驗的機會。虛擬社區，便是簡化了的社會模型！網上遊戲The Sims Online，已成為社會學家一個有趣的觀察平台。由此，社會學可名正言順的稱為社會科學（social science）。

有教無類

與一位資深人士談天，認為教育署提倡『融合教育』　－　把殘障學生放入一般學校　－　是好心做壞事，被虛無的『有教無類』害苦了。

但『有教無類』，是指對所有學生都同樣的用心去教，而不是指對所有學生都用同樣方法來教！有教無類，若不能配合『因材施教』，當然事倍功半！

現實是，根本沒有學校有足夠資源來因材施教，一般學生因程度不同產生的問題也難解決，所以我們才要把學生分級。至於標籤效應，是無奈的社會現實。

融合教育，和把學生分級相反，是把有不同需要的學生放在一起，這當然要投入大量資源，但這究竟符不符合社會效益？

或者，鼓勵不同學校（包括一般學校，特殊學校，及其他）多作課外交流，會不會是個更好的選擇？

作為研究，教育理論是最困難。大多數教育理論都是紙上談兵，沒有多少實驗數據支持；皆因那個家長會在有其他可行方法的情況下，容許自己的孩子作實驗室的白老鼠？除非是政府帶頭作試驗，但一不小心，就是政治事件，香港的教育改革便是證明！

在社會學的其他範圍，因互聯網的出現而令實驗變得可行，在虛擬世界可容易創造出不同的網上社會；但教育理論的測試，目前仍可說是舉步為艱！

類同，同類

峰人風語在《另外與例外》中，以為alternative一詞把「另類」的概念演繹得很出色。但中文的「類」字本身亦很有趣：放於名詞之後，便可引為同類；放於名詞之前，便是似而不同。

類人猿是像人的猿。

類白蛋是似蛋白質的化合物。

類星體是似星星（恒星）的太空物體。

不知類固醇名稱由來？

如果我們不說「偽科學」或「偽氣功」，而說「類科學」或「類氣功」，會否厚道一點？

正如我們不說「假唐三彩」，而說「仿唐三彩」，總之要人知道不是「唐三彩」便成了！

若我們說中國是「類民主」，而非「假民主」，領導人會否順氣點？

噢，這篇文章類同無厘頭，實與廢話同類！

突然感想：其實香港學生早知求學不是求「分數」，而是求「分類」　－　考試成績是A類、B類、C類、...、F類；學業成績是Band 1 類、Band 2 類、Band 3 類；大學畢業是一級榮譽類、二級榮譽類、三級榮譽類；等等．．．．唉！這和有教無類是否背道而馳？

物以類聚

上篇《抽象的無厘頭》談及數學中稱為『類』的概念，不容易理解。

其實不論在任何學問，分類也是個難搞的問題。不良的分類系統，會令研究、分析、及應用變得因難。而隨着社會及認知的改變，分類系統亦要與時俱進。

最常接觸的分類問題，首選市埸學。若在糧油雜貨的地方賣書，可能只是笑話而已；但若在公共屋邨經營高級時裝店，不虧本才怪！

圖書館學當然以分類學為核心，不過金融數學的書應放在金融學還是數學的書架呢？

化學的分類，以往建基於外形特質，現在改由分子結構決定。化學最基本的是原子，目前以原子結構（電子分佈）排列，叫作元素周期表。一般元素周期表是二維平面，其實可以是個三維立體：
生物學的分類，其轉變之速令人詫異，這歸功於突飛猛進的DNA序列科技。誰估到蹄免（hyrax，下圖）竟與大象是近親？


語言分類學的分類亦不容易，苗族和瑤族的語言，是漢藏語系的分支，或是獨立語系，亦有很大爭議。

當然所有的分類學中，最最最困難的是把人分類，皆因隨時可引致岐視或沖突。香港政府把學生分為五級或三級，已可以成為社會問題，這就是明證罷。

抽象的無厘頭

所謂萬數皆集，現今數學已可把大部分的數學物件轉化為「集合」－簡單來說，集合就是一堆堆東西。

而然，因邏輯原因，不能隨便把東西放在一起成為集合。例如沒有包含所有集合的集合。

基於同一原因，不能隨意把同類的集合放在一起成為新的集合。但數學家仍希望把同類的集合放在一起研究，於是他們把同類的集合放在一起，組成一個新的數學物件　－　「類」（class）。

『凡事都有例外』。類，作為數學物件，並不是集合。因為邏輯限制，類的應用比集合論困難；類的抽象，使得多數時候，還是要回歸集合論以解決問題。

但掌握了類，則大大增強數學的深層認知。

因為類的邏輯比集合的邏輯更難，類的抽象比集合的抽象更難掌握，類理論被謔稱為『抽象的無厘頭』（Abstract nonsense）。

抽象的無厘頭，與笑匠周星馳的無厘頭一樣，是有的放矢，要經過精心計算的！

萬『數』皆『集』

道家曰：萬物為一。
佛家曰：萬法皆空。

數學家曰：萬數皆集！

道家及佛家的說法是以形而上學解答問題；數學家剛好相反，是希望避免形而上學。

在文明之初：數目生於實用，圖形始於美學；

隨時間演進：建築、天文、農耕、稅收等，產生新的數學，亦把各種數學枝派連繫起來；

宗教的數學：由天文與占卜，把數學引入宗教內；古希臘人，古印度教，古馬雅，以及易經等，都把數學賦與一定的神秘地位；

科技的發展：經濟及科技的火速發展，令數學的重要性大大增加，亦令『數學是甚麼？』的問題愈趨迷惑。而各種數學枝派，卻未能有效的連繫，冀望有一套共同的數學語言。　

集合，是數學家康托爾為研究無限所創造的概念。簡單來說，一個集合就是一堆東西。小學生也懂的温氏圖（見下圖），就是集合的最簡單表逹法。



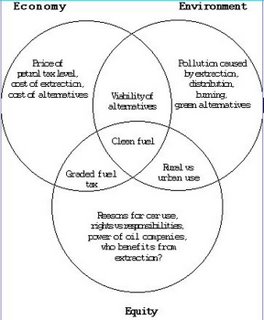
集合所載的，不用是實物：可以是一個個的數字，可以是一種種的思想，可以是一層層的概念。

慢慢地，數學家把幾乎所有的抽象數學物件，變成了一個個的集合。譬如上一篇《零與空》，便提到０是一個甚麼都沒有的集合。集合論的語言，逐步成為所有數學的共同語言。

『數學是甚麼？』在很多時候，都可變成『集合是甚麼？』。集合，就是一堆東西，看來是個非常堅實而簡明的概念，而絕大多數數學家，都可以安安樂樂的，不需要再考慮形而上學的問題。

但危險卻出現，這就是羅素悖論，最形象化的是如下問題：一個「要給所有不自已理髮的人理髮，不給任何自己理髮的人理髮」的理髮師，會不會為自己理髮？

這個例子，生動的說明不是所有的條件都可以運用；對數學來說，即不是隨便把東西放在一起，邏輯上就可以行得通。

二十世紀初的殺着，就是公理化　－　所有數學定理，由最基本的數條『公理』（即可行假設）經邏輯推論而來。於是數學變成了純粹的推理遊戲，杜絕了除便給與條件的運用問題；同時解決『集合是甚麼？』，答案是一些符號而已！

對於最深入的哲理問題，當然仍有哲學家及基礎數學家在努力鑽研（他們認為集合論仍有一些缺點，需要替代或改良）。但『萬數皆集』已是目前最一般的共識！

零與空

『空』是甚麼？

這是個哲學問題，我不懂答，亦不敢答。

『零』是甚麼？

這是個似乎是相類的哲學問題，但．．．

在最最最初的時候，０只是用以區分 70 及 700 等數字的符號。

隨着負數的引入，加減乘除的法則往往要根據數值的正負來分類，《九章算經》便是一例。把０作數字看待，便可大大簡化四則運算的規則。事實上，確是意大利商人為着會計便利，不顧統治者對羅馬數字的眷戀，大力推動阿拉伯數字－包括０－的應用。在此，我們要向歷史上最早的會計師致敬！

但，正數代表擁有，負數代表欠缺，０呢？０代表沒有，但既然沒有，又何需代表！

對印度教，佛教，或道教，『有』與『沒有』只是事實的兩面，倒沒甚大不了。

對馬雅人，他們沒有正負數的認知，但他們認為第０日是世界終結或開始，可不容易應付。他們０的符號，倒是最美麗的！


馬雅文化其中兩個０的符號

對中古時的歐洲人，『神』是『創造』，是『有』；『沒有』不是和神相反嗎？

不明白，但好用，０是在爭議聲中成為數學重要的一員。

幸好，數學家有一個解決方法，在公理代系統內，把０看作是自然數的起始點　－　簡單點說，０只是個數學符號而已，會因應不同實際用途給與不同意義。其他自然數１，２，３等，亦作如是觀。畢竟，１，２，３等並非存在於俗世的東西。

溤‧諾伊曼（John von Neumann）提出把０定義為『空集』，這是一個數學慨念，但可以實體化的看作是『空空如也的袋子』：注意是『空空如也的袋子』，不是『空空如也』！

如貴婦狗、狼狗、西施狗，都可稱為狗；空的袋、空的碗、空的錢包，都可喚作零！

這雖不能解決所有問題，但已可解決大多數的問題。

所以０不是『沒有』，亦不是『無』，也不是『空』。

我不是玩弄文字遊戲，日常的『沒有』，道教的『無』，及佛學的『空』，是三個不同的慨念啊！

不存在的『空間』

半杯水，可以看作一半滿或一半空，視乎觀點學⻆度。不過那一半空間，事實充滿水蒸氣。

『留白 』，可以視作在佈滿色彩的作品中留下一點兒空白，但其實也是在空白的紙張上加一點色彩。不過白色，也是一種顏色。

太空，有一個個獨立星系放在太虛中，但從極大尺度看，也可以是一個個空洞放入充滿物質的世界中。不過有人相信宇宙主要由看不見的暗物質組成，亦相信真空其實充滿瞬間消失的虛粒子。

如是，並沒有真正的空間。『空』，可能只存在於我們的思想之中。

說得太多『空』，自己也開始覺得空洞。不若我們一說另類的空間，數學的空間。

數學中，一堆『物件』加上某種聯系，便可稱為空間。例如平面空間便是｛(x,y) : x,y ∈ ℜ} 配上加法 (x,y)+(w,z)=(x+w,y+z) 及距離 ((x-w)²+(y-z)²)^1/2。

單獨看，數學空間好像不代表甚麼，但在實際應用時，有不同的意義：歐基里德空間－牛頓物理中，『物件』代表一個個時空的位置；慨率空間－計算機會時，『物件』是一件件可能發生的事；希爾伯特空間－量子力學裡，『物件』是粒子的不同狀態。

但若然拋開它的實用意義，數學空間是甚麼呢？

有一派認為所有數學物件都是真實存在（數學存在主義 Mathematical Realism）。

或者，最最最簡單的，數學空間只是研究結構的一種語言及一種思考方式！

你沒有留白！

有朋友笑說我上篇《美麗的『空白』》中沒有留白。當然囉，我在文章中說留白要有功力，但我的功力不夠嘛！

或者可能我的風格太學術性　－　學術性文章一般較注重細節；注重細節則沒有多少留白的餘地；沒有留白或者規限了讀者的思想；規限了思想便會沉悶！

但為甚麼有些人對學術性文章看得津津有味呢？

我的答案是：因為他們本身已有一定基礎，容易產生共鳴，在腦海中自動形成思想空間，即是自助『留白』！

舉例說：弗洛伊德的《夢的解析》及馬克思的《資本論》都是經典，但究竟有多少非學者真的看過？

相似的，對大多數學生，數學證明令人頭痛，但偏偏數學家口中有『美麗的證明』。

還有：吵耳的中國戲曲很悅耳，醜陋的昆蟲（以至蟑螂）很有趣，擠迫的建築群很有草根風味，等等。

最懂得留白的是政客，他們時常開空頭支票，給人無限憧憬．．．