無限的大

在 《零與空》中，我說把０看作一個空的袋子，而不是空，可把形而上學的味道減至最小。朋友笑說：若是個無限大的袋子，那未不是和虛空一樣嗎？

當然，整個宇宙根本不是無限大，所以沒有無限大的袋子。

其實，『無限大』是甚麼？有信仰的人士可能會說他的神就是無限大，但科學的應用需要的是世俗的無限大。康托爾（Georg Cantor）率先對數學上無限大下定義，並由此創造出集合論。

不同的宗教有不同的神，即使同一宗教也可能有不同等級的神。

除着研究的深入，數學家發現不同的系統有不同的無限，即使同一系統內也可有不同大小的無限。

讓我們先看看康托爾的無限，即由比較多少引申出來的無限：

在《自然的數？》中， 我說 0={ }，1={0}，2={0,1}， 3={0,1,2}，4={0,1,2,3}，．．．。可以見到 0 <1 <2 <3 <4 <5 <...。把所有自然數放在一起，有N={0,1,2,...}，得0 < 1 <2 <... <N。

把整條數線列出來（記作ｃ），除自然數外還有很多數字，所以 N < c。 c 當然也是無限。

就這樣，可看到有兩個不同的無限。當然，還可以不停引申下去。

接着，讓我們看看由數字大小引申出的無限：

我們最熟悉的無限莫如 ∞ 及 -∞，是甚麼呢？基本上，這只是兩個符號，∞ 表示比任何正數都正，-∞ 表示比任何負數都負。它倆都不是數，因為不能進行四則運算。而 ∞ 及 -∞ 是數線的兩極，直如祆教中陰陽兩個神衹，有你冇我！


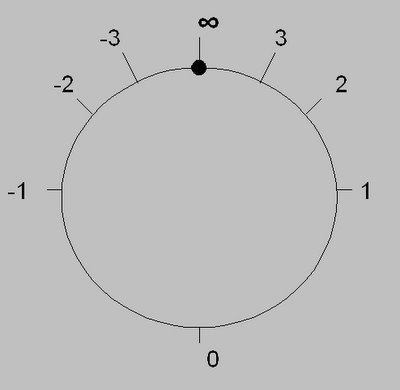
不過若我們把正無窮與負無窮都看作是同一個無限 ∞ ，我們得到一個環，稱為數線的“一點緊化”（one point compactification），就有些中國哲理「物極必反」的味道，因正的盡頭便是負！雖然 ∞ 也是一個無限，但與其他數字都只是環上的一點，失去了某些特殊性。


把無限賦與一般數字性質的是Abraham Robinson，他的系統內有無限個無窮大，若 x，y 是不同的無窮大（即比所有數字都大），則x+2，3y，x+y等，都是不同的無窮大；而-x，-y則是不同的負無窮大（即比所有負數都負）；1/x，1/y則是不同的無窮小（即不是0，卻比所有正數都小）。

唔，不論任何情形，都沒有1/0啊！所以盡量不要說1/0=∞！