朋友說我近期寫的太難太深,這可是我的老毛病。
不過,這也是數學的問題。
我寫的,只算是現代數學基礎,但基礎不等於容易。
情形等於:化學的基礎在原子,物理的基礎在能量,經濟的基礎在交易資本。
科學之所以難,因為學習的起點是在中間出發,而不是由基礎結構開始。原因是基礎構不能通過感觀接觸了解。一個學術的基礎結構並不是該學術的基礎學問!
一個永恆的教育難題,是在甚麼時候開始教導教基礎結構。
Sunday, April 30, 2006
Friday, April 21, 2006
數字是個遊戲
『數字是個遊戲。』誰人會說這樣的話?
一個見慣風浪,歷盡起跌的股壇老手?
一個不負責任,專個假賬的會計敗類?
一個腰纏萬貫,勝負等閒的商界巨賈?
一個強作瀟洒,生活平實的過氣富翁?
一個活動教學,負責數學的小學老師?
若通通不是,可能這人是個研究組合遊戲理論的數學家。
組合遊戲理論是研究純技術的博奕遊戲,例如圍棋、象棋、拿火柴遊戲。麻將、飛行棋、天九等不在其研究範圍;橋牌、鋤大弟、十三張等也不在其研究範圍--因要猜對方手中的牌,也有運氣成分。數學家主要是研究二人博奕。
Ernst Zermelo (1871-1953) 率先證明所有二人博奕都應是早知結果的!要麼是先行者有必勝(應是不敗)策略,要麼是後行者有必勝方法,這當然視乎是何類遊戲。(見〔1〕)

約翰.康威(John H. Conway)提出了個有趣的定義:一個 (L|R) 是個遊戲如果 L 及 R 也是個遊戲--這定義可用於尋找必勝策略。他與兩位重量級人物在著作《穩操勝券(上下冊)》(Winning Ways for your Mathematical Plays)有講述這定義的應用,這本書在一般書局有售。
若然限制 L < R(何謂大小,這不贅),就是超實數 surreal numbers,一種包含無限大及無窮小的數字系統!這個慨念是建基於Dedekind cuts,本來用於透過分數定義實數。
所以,『數字是個遊戲。』可是有真正數學意義的啊!
一個見慣風浪,歷盡起跌的股壇老手?
一個不負責任,專個假賬的會計敗類?
一個腰纏萬貫,勝負等閒的商界巨賈?
一個強作瀟洒,生活平實的過氣富翁?
一個活動教學,負責數學的小學老師?
若通通不是,可能這人是個研究組合遊戲理論的數學家。
組合遊戲理論是研究純技術的博奕遊戲,例如圍棋、象棋、拿火柴遊戲。麻將、飛行棋、天九等不在其研究範圍;橋牌、鋤大弟、十三張等也不在其研究範圍--因要猜對方手中的牌,也有運氣成分。數學家主要是研究二人博奕。
Ernst Zermelo (1871-1953) 率先證明所有二人博奕都應是早知結果的!要麼是先行者有必勝(應是不敗)策略,要麼是後行者有必勝方法,這當然視乎是何類遊戲。(見〔1〕)

約翰.康威(John H. Conway)提出了個有趣的定義:一個 (L|R) 是個遊戲如果 L 及 R 也是個遊戲--這定義可用於尋找必勝策略。他與兩位重量級人物在著作《穩操勝券(上下冊)》(Winning Ways for your Mathematical Plays)有講述這定義的應用,這本書在一般書局有售。
若然限制 L < R(何謂大小,這不贅),就是超實數 surreal numbers,一種包含無限大及無窮小的數字系統!這個慨念是建基於Dedekind cuts,本來用於透過分數定義實數。
所以,『數字是個遊戲。』可是有真正數學意義的啊!
Thursday, April 20, 2006
超越現實的數
不懂數學的人, 可能也會接受無限大及無窮小;反而對數學家,接受無限大及無窮小會有邏輯上的問題。
當Abraham Robinson成功創造出包含無限大和無窮小,且邏輯上可行的數字系統,在數學界產生頗大迴響。這系統是 hyperreal numbers。最簡單的解釋,系統內每個數其實是個數列--7 是 (7,7,7,...) 而 -8 是 (-8,-8,...,-8);無限大是不斷增大的數列,如 (1,2,3,4,...) 及 (1,3,5,7,...) 便是兩個無限大;無窮小是愈來愈接近0的數列,如 (1,1/2,1/3,1/4,...) 及 (1,0.1,0.01,0.001,...)便是兩個無窮小。當然還有其他理論上的限制。
稍後, John Horton Conway發明了另一套數字系統,也包含無限大和無窮小,產生的不是迴響,而是震撼!這系統是 surreal numbers。Conway 運用了載得金分割(Dedekind cuts)的意念,成功的把現代數學中多個不同的範疇(實數,序數,組合理論)連繫起來。很難三言兩語說明 Conway 的理論解釋,但可以說的是,他證明了『數字是個遊戲』!事實上,Conway 發展這理論真的是要研究一種遊戲--我國的國技『圍棋』!!!
可能是遺撼,兩者的中文名稱都是超實數。還有另一個超實數 superreal numbers,是 hyperreal numbers 的再擴張。
某程度來說,日常生活中或許不會遇到這些數,超實數可謂名副其實;但從數學上而言,超實數與實數同樣真實。
當Abraham Robinson成功創造出包含無限大和無窮小,且邏輯上可行的數字系統,在數學界產生頗大迴響。這系統是 hyperreal numbers。最簡單的解釋,系統內每個數其實是個數列--7 是 (7,7,7,...) 而 -8 是 (-8,-8,...,-8);無限大是不斷增大的數列,如 (1,2,3,4,...) 及 (1,3,5,7,...) 便是兩個無限大;無窮小是愈來愈接近0的數列,如 (1,1/2,1/3,1/4,...) 及 (1,0.1,0.01,0.001,...)便是兩個無窮小。當然還有其他理論上的限制。
稍後, John Horton Conway發明了另一套數字系統,也包含無限大和無窮小,產生的不是迴響,而是震撼!這系統是 surreal numbers。Conway 運用了載得金分割(Dedekind cuts)的意念,成功的把現代數學中多個不同的範疇(實數,序數,組合理論)連繫起來。很難三言兩語說明 Conway 的理論解釋,但可以說的是,他證明了『數字是個遊戲』!事實上,Conway 發展這理論真的是要研究一種遊戲--我國的國技『圍棋』!!!
可能是遺撼,兩者的中文名稱都是超實數。還有另一個超實數 superreal numbers,是 hyperreal numbers 的再擴張。
某程度來說,日常生活中或許不會遇到這些數,超實數可謂名副其實;但從數學上而言,超實數與實數同樣真實。
Wednesday, April 19, 2006
虛與實,數系的發展
上古時,人只懂1,2,3,...--這是他們的數。
然後,他們需要細分物件,於是出現分數,即兩數之比 a/b--他們認為原先的1,2,3,...才是實在的數,現稱自然數。
然後,有些數量(例如某些長度),是不可以寫成分數--他們(古希臘畢達哥拉斯學派)認為原先的分數才是實在的數,而新發現的數是假的數,傳說中他們甚至殺死Hippasus(第一個發現無理數的人)。分數的希臘文λογος ,意為「成比例的數」(rational number),中文錯譯為有理數,沒理由的數,但這與古希臘人的想法暗合。新發現的數,即「不成比例的數」(irrational number)被譯為無理數。
然後,在尋找多項式 a0+a1x+a2x²+...+anxⁿ=0 的根,不可避免遇到負數的開方--他們認為原先的數(不論有理數或無理數)才實在,是實數,而負數的開方是虛無的數,即虛數。實數與虛數相加,稱為複數。
但後來發現:複數 x+√-1 y 可看作平面上的一點 (x,y),是個二元的數。由此看來,複數非常實在。
數學家開始放開虛實的迷思,得出四元數、八元數、p-進數、超實數、超複數。
但『數』是甚麼?在乎你需要甚麼!
然後,他們需要細分物件,於是出現分數,即兩數之比 a/b--他們認為原先的1,2,3,...才是實在的數,現稱自然數。
然後,有些數量(例如某些長度),是不可以寫成分數--他們(古希臘畢達哥拉斯學派)認為原先的分數才是實在的數,而新發現的數是假的數,傳說中他們甚至殺死Hippasus(第一個發現無理數的人)。分數的希臘文λογος ,意為「成比例的數」(rational number),中文錯譯為有理數,沒理由的數,但這與古希臘人的想法暗合。新發現的數,即「不成比例的數」(irrational number)被譯為無理數。
然後,在尋找多項式 a0+a1x+a2x²+...+anxⁿ=0 的根,不可避免遇到負數的開方--他們認為原先的數(不論有理數或無理數)才實在,是實數,而負數的開方是虛無的數,即虛數。實數與虛數相加,稱為複數。
但後來發現:複數 x+√-1 y 可看作平面上的一點 (x,y),是個二元的數。由此看來,複數非常實在。
數學家開始放開虛實的迷思,得出四元數、八元數、p-進數、超實數、超複數。
但『數』是甚麼?在乎你需要甚麼!
虛(數)與實(數)
以下是兩個常見的數學謎語:
1. 背着喇叭;
2. 大夫診症;
謎底稍後揭曉。
在中學時期,我們知道 ax² +bx+c=0 的兩個解可表達成 (-b ± √ (b² -4ac))/2。
原來 ax³ +bx² +cx+d=0 的三個解也有一般表達式,最簡單的一個是
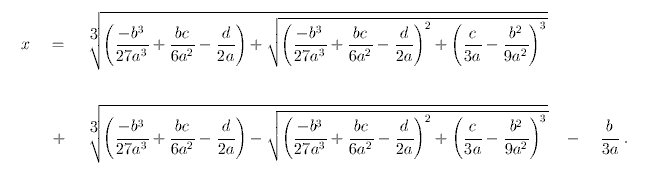
這個解在十六世紀時經已被發現,但卻出現了個問題:考慮 x³ -15x-4=0,它的所有答案是 -3.73, -0.26, 4。若用以上的算式,卻出現不知所謂的 √-109(用計算機試試,九成會送你一個 Error),這條算式似乎用不着!
數學家的解決方法很簡單,首先讓 √-109 = i √109 (這裡i=√-1),然後把i當作一般數字來計,最後所有i會相互抵消!但如 i √109 般的數,令人感覺虛無飄眇,故稱作『虛數』。
這時,人們倒過來說一般的數字是『實數』,即是實在的數。
但正如自然數並不比其他數自然¹,實數的『實』和虛數的『虛』相差其實不大。若考慮二維平面,實數與虛數只是橫軸與縱軸之分而已!
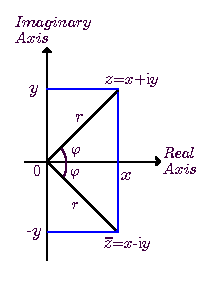 這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
謎語答案:1. 負號;2. 開方。
正數加上負號再開方,便是虛數!
註1:請參看《自然的數?》。
註2:開方只取“正值”,如√4=2但4的平方根是 ±2,這兒 -4 的平方根是 ±2i,2i 的平方根是 ±(1+i),3-4i 的平方根是 ±(2-i)。
1. 背着喇叭;
2. 大夫診症;
謎底稍後揭曉。
在中學時期,我們知道 ax² +bx+c=0 的兩個解可表達成 (-b ± √ (b² -4ac))/2。
原來 ax³ +bx² +cx+d=0 的三個解也有一般表達式,最簡單的一個是
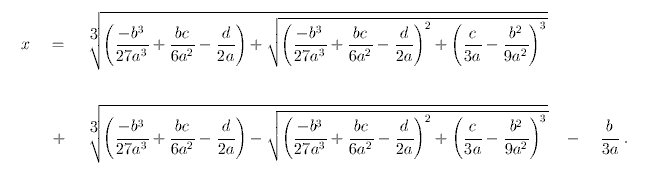
這個解在十六世紀時經已被發現,但卻出現了個問題:考慮 x³ -15x-4=0,它的所有答案是 -3.73, -0.26, 4。若用以上的算式,卻出現不知所謂的 √-109(用計算機試試,九成會送你一個 Error),這條算式似乎用不着!
數學家的解決方法很簡單,首先讓 √-109 = i √109 (這裡i=√-1),然後把i當作一般數字來計,最後所有i會相互抵消!但如 i √109 般的數,令人感覺虛無飄眇,故稱作『虛數』。
這時,人們倒過來說一般的數字是『實數』,即是實在的數。
但正如自然數並不比其他數自然¹,實數的『實』和虛數的『虛』相差其實不大。若考慮二維平面,實數與虛數只是橫軸與縱軸之分而已!
 這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。
這平面稱作複平面,上面的每一點(x,y)代表着x+iy,喚作複數。由此,二維的數出現了,標誌着數字家族新的一頁。在複平面上,『任何複數都有平方根』(e.g. √-4 = 2i,√(2i)=1+i,√(3-4i)=2-i)²,並有着很多不可能在實數出現的特性。謎語答案:1. 負號;2. 開方。
正數加上負號再開方,便是虛數!
註1:請參看《自然的數?》。
註2:開方只取“正值”,如√4=2但4的平方根是 ±2,這兒 -4 的平方根是 ±2i,2i 的平方根是 ±(1+i),3-4i 的平方根是 ±(2-i)。
Monday, April 17, 2006
天與地,大與小,冷與熱
『道可道,非常道;名可名,非常名。』--這是《道德經》 的第一句,亦是最耳熟能詳的一句。我想說說:名可名,非常名。
若我們的祖先把「天」喚作「地」,而把「地」喚作「天」,那未現在便會是“地在上,天在下”了。相類的情況是,不同是事物,喚作一樣的名稱,如「天花」是指一種傳染病或是指屋頂底部,所以要清楚名字背後的意義。
原來,這是學生學習數學的一個大障礙!
名稱的改變:-
首先是代數,是以符號代數字,從而達到一般化的運用。卻出現明白3×(4+2)=3×4+3×2,卻不明白 x(y+z)=xy+xz。
然後是最優化,教了學生怎樣求得最大值,他們卻往往未能舉一反三地求出最小值。大與小,很多時只是換個名稱而已!
定義(含義)的不同:-
首先是關係,不同的場合,大小的定義可能完全不同。一般來說,我們會說 4>2>1>-3;但這並非絕對!
在玩橋牌的時候,我們有1>4>2;在玩“鋤大弟”的時候,我們知道 2>1>4。但若我們不提橋牌,不提鋤大弟,而只說 1>4>2 或 2>1>4,學生會頓時不知所措!!!
在物理學中,若以 K 為温度單位,負温度會比正温度為熱。若以>表示比較熱,則有-3>4>2>1!
然後是擴張,隨着認知深化,需要擴張定義符合實況。在初學複數時,學生仍會給舊認知 “沒有「數」的平方是負數” 所跘着,不理解「數」的定義已改變。
在高級代數書中,a1=a=1a並不單是表示數的乘法(a× 1=a=1× a),亦可表示數的加法(a+0=a=0+a),用意是把「乘法」擴張以覆蓋所有性質相近的運算,減省研究的重複性。可想而知,學生多數未能了解。
在中學物理學中,我們是以温度定義冷熱,但大學時,我們以能量流向定義冷熱。
***********************
在文學中,「名」也有難題。在一些文化中,一個人往往有着不同的稱謂,或者一個家族不同人有相同的名稱,令記性不大好的人(如在下)難於閱讀相關傳記或小說!
例如,三國演義中,一人往往有着三個或以上的稱呼,如諸葛亮,字孔明,號臥龍先生;
又如世界首富比爾蓋茨(William Henry Gates III)的父親也是比爾蓋茨(William Henry Gates, Sr.)!
科學與文學中的「名」已這麼難掌握,更何況哲學中的「名」?
若我們的祖先把「天」喚作「地」,而把「地」喚作「天」,那未現在便會是“地在上,天在下”了。相類的情況是,不同是事物,喚作一樣的名稱,如「天花」是指一種傳染病或是指屋頂底部,所以要清楚名字背後的意義。
原來,這是學生學習數學的一個大障礙!
名稱的改變:-
首先是代數,是以符號代數字,從而達到一般化的運用。卻出現明白3×(4+2)=3×4+3×2,卻不明白 x(y+z)=xy+xz。
然後是最優化,教了學生怎樣求得最大值,他們卻往往未能舉一反三地求出最小值。大與小,很多時只是換個名稱而已!
定義(含義)的不同:-
首先是關係,不同的場合,大小的定義可能完全不同。一般來說,我們會說 4>2>1>-3;但這並非絕對!
在玩橋牌的時候,我們有1>4>2;在玩“鋤大弟”的時候,我們知道 2>1>4。但若我們不提橋牌,不提鋤大弟,而只說 1>4>2 或 2>1>4,學生會頓時不知所措!!!
在物理學中,若以 K 為温度單位,負温度會比正温度為熱。若以>表示比較熱,則有-3>4>2>1!
然後是擴張,隨着認知深化,需要擴張定義符合實況。在初學複數時,學生仍會給舊認知 “沒有「數」的平方是負數” 所跘着,不理解「數」的定義已改變。
在高級代數書中,a1=a=1a並不單是表示數的乘法(a× 1=a=1× a),亦可表示數的加法(a+0=a=0+a),用意是把「乘法」擴張以覆蓋所有性質相近的運算,減省研究的重複性。可想而知,學生多數未能了解。
在中學物理學中,我們是以温度定義冷熱,但大學時,我們以能量流向定義冷熱。
***********************
在文學中,「名」也有難題。在一些文化中,一個人往往有着不同的稱謂,或者一個家族不同人有相同的名稱,令記性不大好的人(如在下)難於閱讀相關傳記或小說!
例如,三國演義中,一人往往有着三個或以上的稱呼,如諸葛亮,字孔明,號臥龍先生;
又如世界首富比爾蓋茨(William Henry Gates III)的父親也是比爾蓋茨(William Henry Gates, Sr.)!
科學與文學中的「名」已這麼難掌握,更何況哲學中的「名」?
Sunday, April 16, 2006
『熱』極必『冷』
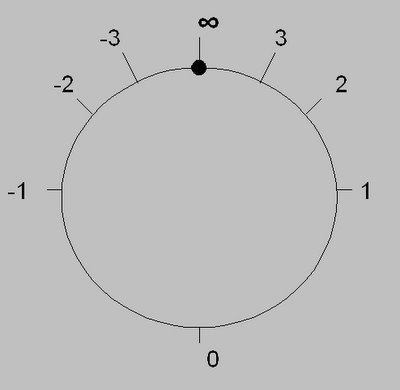
當數線兩端相接,正的盡頭便是負,有中國哲理「物極必反」味道。
物理學上,也有一個古怪現象:若温度不斷提高,在超越無限高温後,温度會變成負數!看來也真有「『熱』極必『冷』」這回事!
但不要給字面騙了,負温度其實比正温度更“熱”!
科學家量度氣温,不是用攝氏 °C 或華氏 °F,而是用開爾文溫標 K。0 K,相當於 -273.15 °C,稱為絕對零度,是低温的極限,一切動能將會消失; 然後1 K = 1 °C,遂級而上,冰點是 273.15 K,太陽表面是 5780 K,太陽中心是 1.3 × 106 K,黑洞温度是1.4×1032 K。
但甚麼是温度?有一個不太簡單的定義是:温度=熵(混亂程度)的變化/能量的變化。一般而言,能量的增加會導致熵的增加,因而有正數的温度;但在某些狀況(最混亂時?),能量增加反而導致熵減少,所以出現負數的温度。
甚麼是冷熱?這是相對的,能量是由較熱處流向較冷處。因為能量會由負温度處流向正温度處,所以負温度比正温度更熱!
當然,我們仍可以用温度的高低來定義冷熱,我們仍可以說「『熱』極必『冷』」,但卻失去如能量流動般的重要物理意義。
Saturday, April 15, 2006
無窮的小
恒古以來,人類便為着物質是無限可分,或有終極結構爭論不休。
古希臘的原子論認為物質是由最小稱為『原子』的東西構成。伴隨着現代化學的誔生,某程度上肯定了原子論。
但化學中的原子,物理學卻仍可分割下去,得出常見的電子、質子、中子,以及μ子、π子、W子、Ω子等等;超弦理論認為還可再分下去,直至達到所謂的超弦結構。
超弦是大小為普朗克單位(Planck units)的物理結構;而普朗克單位,被視為是測量的下限。在普朗克時間(5.39121 × 10-44 s)及普朗克尺度(1.61624 × 10-35 m)內,前與後、左與右亦沒有物理意義。
當前最heat的topic,即納米技術,是以納米(1 nm= 10–9m)為基礎的技術,其實在物理學中不是太小。
普朗克尺度非常小,比佛家的“刹那”還要小,但始終是有限的小,不是『無窮小』。無窮小,是個大於零卻小於任可正數的量,給人難以捉摸的印象;事實上,當數學家最初使用無窮小時,亦困於其邏輯難關,但仍決定實用先行。
當時有名的思想家貝克箂主教對無窮小的應用,作出頗嚴厲的批判;稍後數學家找出方法,可以繞過無窮小,亦令無窮小的議論趨向沈寂。
上世紀中期,Abraham Robinson提出新的數學系統--超實數系統(hyperreal numbers),包含了不同的無限大及無窮小,而且解決了邏輯問題。但沒有無窮小的數學已是主流,新的數學被稱為『非標準分析學』。
在超實數系統中,0.999..... ≠ 1!!!兩數的相差,便是個無窮小。
古希臘的原子論認為物質是由最小稱為『原子』的東西構成。伴隨着現代化學的誔生,某程度上肯定了原子論。
但化學中的原子,物理學卻仍可分割下去,得出常見的電子、質子、中子,以及μ子、π子、W子、Ω子等等;超弦理論認為還可再分下去,直至達到所謂的超弦結構。
超弦是大小為普朗克單位(Planck units)的物理結構;而普朗克單位,被視為是測量的下限。在普朗克時間(5.39121 × 10-44 s)及普朗克尺度(1.61624 × 10-35 m)內,前與後、左與右亦沒有物理意義。
當前最heat的topic,即納米技術,是以納米(1 nm= 10–9m)為基礎的技術,其實在物理學中不是太小。
普朗克尺度非常小,比佛家的“刹那”還要小,但始終是有限的小,不是『無窮小』。無窮小,是個大於零卻小於任可正數的量,給人難以捉摸的印象;事實上,當數學家最初使用無窮小時,亦困於其邏輯難關,但仍決定實用先行。
當時有名的思想家貝克箂主教對無窮小的應用,作出頗嚴厲的批判;稍後數學家找出方法,可以繞過無窮小,亦令無窮小的議論趨向沈寂。
上世紀中期,Abraham Robinson提出新的數學系統--超實數系統(hyperreal numbers),包含了不同的無限大及無窮小,而且解決了邏輯問題。但沒有無窮小的數學已是主流,新的數學被稱為『非標準分析學』。
在超實數系統中,0.999..... ≠ 1!!!兩數的相差,便是個無窮小。
Thursday, April 13, 2006
無限的大
在 《零與空》中,我說把0看作一個空的袋子,而不是空,可把形而上學的味道減至最小。朋友笑說:若是個無限大的袋子,那未不是和虛空一樣嗎?
當然,整個宇宙根本不是無限大,所以沒有無限大的袋子。
其實,『無限大』是甚麼?有信仰的人士可能會說他的神就是無限大,但科學的應用需要的是世俗的無限大。康托爾(Georg Cantor)率先對數學上無限大下定義,並由此創造出集合論。
不同的宗教有不同的神,即使同一宗教也可能有不同等級的神。
除着研究的深入,數學家發現不同的系統有不同的無限,即使同一系統內也可有不同大小的無限。
讓我們先看看康托爾的無限,即由比較多少引申出來的無限:
在《自然的數?》中, 我說 0={ },1={0},2={0,1}, 3={0,1,2},4={0,1,2,3},...。可以見到 0 <1 <2 <3 <4 <5 <...。把所有自然數放在一起,有N={0,1,2,...},得0 < 1 <2 <... <N。
把整條數線列出來(記作c),除自然數外還有很多數字,所以 N < c。 c 當然也是無限。
就這樣,可看到有兩個不同的無限。當然,還可以不停引申下去。
接着,讓我們看看由數字大小引申出的無限:
我們最熟悉的無限莫如 ∞ 及 -∞,是甚麼呢?基本上,這只是兩個符號,∞ 表示比任何正數都正,-∞ 表示比任何負數都負。它倆都不是數,因為不能進行四則運算。而 ∞ 及 -∞ 是數線的兩極,直如祆教中陰陽兩個神衹,有你冇我!

不過若我們把正無窮與負無窮都看作是同一個無限 ∞ ,我們得到一個環,稱為數線的“一點緊化”(one point compactification),就有些中國哲理「物極必反」的味道,因正的盡頭便是負!雖然 ∞ 也是一個無限,但與其他數字都只是環上的一點,失去了某些特殊性。

把無限賦與一般數字性質的是Abraham Robinson,他的系統內有無限個無窮大,若 x,y 是不同的無窮大(即比所有數字都大),則x+2,3y,x+y等,都是不同的無窮大;而-x,-y則是不同的負無窮大(即比所有負數都負);1/x,1/y則是不同的無窮小(即不是0,卻比所有正數都小)。
唔,不論任何情形,都沒有1/0啊!所以盡量不要說1/0=∞!
當然,整個宇宙根本不是無限大,所以沒有無限大的袋子。
其實,『無限大』是甚麼?有信仰的人士可能會說他的神就是無限大,但科學的應用需要的是世俗的無限大。康托爾(Georg Cantor)率先對數學上無限大下定義,並由此創造出集合論。
不同的宗教有不同的神,即使同一宗教也可能有不同等級的神。
除着研究的深入,數學家發現不同的系統有不同的無限,即使同一系統內也可有不同大小的無限。
讓我們先看看康托爾的無限,即由比較多少引申出來的無限:
在《自然的數?》中, 我說 0={ },1={0},2={0,1}, 3={0,1,2},4={0,1,2,3},...。可以見到 0 <1 <2 <3 <4 <5 <...。把所有自然數放在一起,有N={0,1,2,...},得0 < 1 <2 <... <N。
把整條數線列出來(記作c),除自然數外還有很多數字,所以 N < c。 c 當然也是無限。
就這樣,可看到有兩個不同的無限。當然,還可以不停引申下去。
接着,讓我們看看由數字大小引申出的無限:
我們最熟悉的無限莫如 ∞ 及 -∞,是甚麼呢?基本上,這只是兩個符號,∞ 表示比任何正數都正,-∞ 表示比任何負數都負。它倆都不是數,因為不能進行四則運算。而 ∞ 及 -∞ 是數線的兩極,直如祆教中陰陽兩個神衹,有你冇我!

不過若我們把正無窮與負無窮都看作是同一個無限 ∞ ,我們得到一個環,稱為數線的“一點緊化”(one point compactification),就有些中國哲理「物極必反」的味道,因正的盡頭便是負!雖然 ∞ 也是一個無限,但與其他數字都只是環上的一點,失去了某些特殊性。

把無限賦與一般數字性質的是Abraham Robinson,他的系統內有無限個無窮大,若 x,y 是不同的無窮大(即比所有數字都大),則x+2,3y,x+y等,都是不同的無窮大;而-x,-y則是不同的負無窮大(即比所有負數都負);1/x,1/y則是不同的無窮小(即不是0,卻比所有正數都小)。
唔,不論任何情形,都沒有1/0啊!所以盡量不要說1/0=∞!
自然的數?
數是甚麼?由遠古開始,1、2、3、...分別是一種東西、二種東西、三種東西...的量化詞,所以這些才是一般人心中的數。但隨着小數,分數等出現,我們把1、2、3、...稱作自然數,即這些才是自然出現的數。
但數學家需要更堅實的定義。
在《萬『數』皆『集』》中,我說每個數都是一個『集合』--可以看成一個袋子。0是空空如也的袋子,1是載着一件東西的袋子,2是載着兩件東西的袋子,如此類推。
0是空空如也的袋子,記作{}。
既然1是載着一件東西的袋子,內裡的東西是甚麼呢?一個包、一件衫、一張相?都可以,就如西施狗、牧羊狗、狼狗都可以代表狗。於是1可以是{包},可以是{衫},可以是{相},但也可以放進一個0,即{0}!
如此類推,2載着0及1,記作{0,1}。3是{0,1,2},4是{0,1,2,3},5是{0,1,2,3,4}。
這樣,可以不假外求,完全在數學內定義出所有0,1,2,...。這些數,是其他數的起點,就是自然數!問題出現了,0似乎不那麼『自然』,它由誔生至被接受成數字需要經過數百年,怎看也不自然吧?!
現在,若把0當自然數,便把1,2,...稱為正整數;若不把0當自然數,便把0,1,2,...稱作非負整數。夠混亂了罷!
不過1,2,...也並非真的這麼自然,亞馬遜河居住的Pirahã族人,其語文根本沒有數字慨念!--數,既然不是必需,或者根本不能說自然!
或者『自然』也是相對的,一些人的自然是另一些人的不自然。
但數學家需要更堅實的定義。
在《萬『數』皆『集』》中,我說每個數都是一個『集合』--可以看成一個袋子。0是空空如也的袋子,1是載着一件東西的袋子,2是載着兩件東西的袋子,如此類推。
0是空空如也的袋子,記作{}。
既然1是載着一件東西的袋子,內裡的東西是甚麼呢?一個包、一件衫、一張相?都可以,就如西施狗、牧羊狗、狼狗都可以代表狗。於是1可以是{包},可以是{衫},可以是{相},但也可以放進一個0,即{0}!
如此類推,2載着0及1,記作{0,1}。3是{0,1,2},4是{0,1,2,3},5是{0,1,2,3,4}。
這樣,可以不假外求,完全在數學內定義出所有0,1,2,...。這些數,是其他數的起點,就是自然數!問題出現了,0似乎不那麼『自然』,它由誔生至被接受成數字需要經過數百年,怎看也不自然吧?!
現在,若把0當自然數,便把1,2,...稱為正整數;若不把0當自然數,便把0,1,2,...稱作非負整數。夠混亂了罷!
不過1,2,...也並非真的這麼自然,亞馬遜河居住的Pirahã族人,其語文根本沒有數字慨念!--數,既然不是必需,或者根本不能說自然!
或者『自然』也是相對的,一些人的自然是另一些人的不自然。
Monday, April 10, 2006
一個數學故事
在某年某月某日,有兩位學者大膽猜測宇宙中存在一個巨大的怪獸群。要證明他們的猜想,展開了漫長的時空搜索。經過多年的努力,他們穿越了一個一一六八八三維的空間,並成功找出了怪獸群,震撼國際。怪獸群果真異常巨大,內個體數目以億兆計,難以作簡單的描述。
後來,有人認定這怪獸群與傳說中不可思議的『怪異月光』有關,又開始了一個大規模的探索。經過不少的艱辛,流過不少汗水,終於有一天,探究者發現了傳說中的『怪異月光』。
多年後,有兩人在討論怪獸群.一個讚嘆道:『這個怪獸群真是不簡單!』另一人搖頭笑說:『不!這個怪獸群真是簡單!』
故事完。
問:為什麼這是一個數學故事? 如果你還在求學,問問你的數學老師。他可能答錯,但不要取笑他,這可不是個容易答的問題啊!答案如下:
 一群怪獸,但不是一個『怪獸群』:P。
一群怪獸,但不是一個『怪獸群』:P。
群 group 是一個數學結構,擁有乘及除兩種運算。群內有群稱作子群 subgroup,沒有所謂正規子群 normal subgroup 的群就是簡單群 simple group。簡單群的結構一般真的簡單,除了廿六個奇怪簡單群(名為零散群 sporadic groups)之外。
兩位數學家Fischer及Griess在1970億測哪個是最大的零散群,將之定名怪獸群 Monster group。七年後終於證實怪獸群的存在,構作方法是利用一個196883維的代數空間。這個怪獸群有8 × 1053個“元素”,真是非常巨大。
怪異月光 monstrous moonshine 是關於怪獸群的另一個特性,即使研究者亦以「怪異」稱之。由Conway及Norton在1979年提出,在1992年被Borcherds證明──Borcherds亦由此獲得數學界最高榮譽菲爾茲奬。
怪獸群毫不簡單,但它畢竟是個簡單群呀!
後來,有人認定這怪獸群與傳說中不可思議的『怪異月光』有關,又開始了一個大規模的探索。經過不少的艱辛,流過不少汗水,終於有一天,探究者發現了傳說中的『怪異月光』。
多年後,有兩人在討論怪獸群.一個讚嘆道:『這個怪獸群真是不簡單!』另一人搖頭笑說:『不!這個怪獸群真是簡單!』
故事完。
問:為什麼這是一個數學故事? 如果你還在求學,問問你的數學老師。他可能答錯,但不要取笑他,這可不是個容易答的問題啊!答案如下:
 一群怪獸,但不是一個『怪獸群』:P。
一群怪獸,但不是一個『怪獸群』:P。群 group 是一個數學結構,擁有乘及除兩種運算。群內有群稱作子群 subgroup,沒有所謂正規子群 normal subgroup 的群就是簡單群 simple group。簡單群的結構一般真的簡單,除了廿六個奇怪簡單群(名為零散群 sporadic groups)之外。
兩位數學家Fischer及Griess在1970億測哪個是最大的零散群,將之定名怪獸群 Monster group。七年後終於證實怪獸群的存在,構作方法是利用一個196883維的代數空間。這個怪獸群有8 × 1053個“元素”,真是非常巨大。
怪異月光 monstrous moonshine 是關於怪獸群的另一個特性,即使研究者亦以「怪異」稱之。由Conway及Norton在1979年提出,在1992年被Borcherds證明──Borcherds亦由此獲得數學界最高榮譽菲爾茲奬。
怪獸群毫不簡單,但它畢竟是個簡單群呀!
Saturday, April 08, 2006
偽學問:是與非
剛拜讀田松博士的《永动机与哥德巴赫猜想》 ,描述的是全世界科學家的一個惡夢:『民間科學家』。
民間科學家是指一些沒經過正統訓練,以貧乏的知識及不成熟的邏輯思維,希望得出對世界具影嚮力的重大發明。他們嘗試制造永動機(幾乎是無中生有的得到能量),三等分任意角(以知不可能的古希臘數學題),及證明哥德巴赫猜想(當令最知名的數學難題)等等。他們即使無數次被科學家指出其錯誤,但仍頑強地研究,並把批評視為無知或打壓。
民間科學家大多是獨立研究,帶着孤獨前鋒的悲壯;但亦有一些得到廣泛支持,結果發展成偽科學(如雙氧水治病,“神化了的”氣功等)。
當然也有一些因為名氣、金錢、宗教等原因,故意推出違背一般科學知識的理論:如莫札特效應,智慧創造論,採光美容等。事實上,這類偽科學的受支持程度,甚至超乎正統科學。
除科學以外,還有很多相似的情況:有人提出中國人先發現新大陸;工會分子積極挑戰經濟學家的理論;不知所謂的行為藝術家。
不過對這些另類理論的支持者,我們反而是頑固的一群。當是與非的感覺倒置了,是與非真的倒置了麼?
民間科學家是指一些沒經過正統訓練,以貧乏的知識及不成熟的邏輯思維,希望得出對世界具影嚮力的重大發明。他們嘗試制造永動機(幾乎是無中生有的得到能量),三等分任意角(以知不可能的古希臘數學題),及證明哥德巴赫猜想(當令最知名的數學難題)等等。他們即使無數次被科學家指出其錯誤,但仍頑強地研究,並把批評視為無知或打壓。
民間科學家大多是獨立研究,帶着孤獨前鋒的悲壯;但亦有一些得到廣泛支持,結果發展成偽科學(如雙氧水治病,“神化了的”氣功等)。
當然也有一些因為名氣、金錢、宗教等原因,故意推出違背一般科學知識的理論:如莫札特效應,智慧創造論,採光美容等。事實上,這類偽科學的受支持程度,甚至超乎正統科學。
除科學以外,還有很多相似的情況:有人提出中國人先發現新大陸;工會分子積極挑戰經濟學家的理論;不知所謂的行為藝術家。
不過對這些另類理論的支持者,我們反而是頑固的一群。當是與非的感覺倒置了,是與非真的倒置了麼?
Monday, April 03, 2006
絕對與相對
朋友在他的《絕對與相對》,又提出「是」一字可產生的問題。奇實自公孫龍白馬非馬以來,關於「是」「非」的語意岐義,已分析過何只千萬次!
科學上,需要嚴防岐義,所以要創造一些符號語言,可算是人類第一套沒有讀音的文字。
「一支筆是文具」:一支筆∈文具;∈表示「其中一個」。
「筆是文具」:筆⊆文具;⊆表示「其中一種」。
「文學創作工具是文具」:文學創作工具=文具;=表示「等如」。
「百無一用是書生」:百無一用(的東西)⊇ 書生;這其實是倒裝寫法,我懷疑「佛教是文學,哲學,科學」本應寫為「文學,哲學,科學皆是佛學」。
「強人是你,能頂天立地」:強人∋ 你;這也是倒裝法。
當然啦,「是」還有其他用法。
「是其是」:第一個「是」意思為「贊成,支持」,第二個「是」意思為「正確的事」;全句為「贊成正確的事」。
當然啦,此乃我極膚淺的分析。很多時候,文學作者故意利用模棱兩可的觀念創作,這也算留白罷!
或者正如我朋友所說,不要時常太執着於正確的意思:世上多數東西都只有「相對正確」,沒有「絕對正確」。
科學上,需要嚴防岐義,所以要創造一些符號語言,可算是人類第一套沒有讀音的文字。
「一支筆是文具」:一支筆∈文具;∈表示「其中一個」。
「筆是文具」:筆⊆文具;⊆表示「其中一種」。
「文學創作工具是文具」:文學創作工具=文具;=表示「等如」。
「百無一用是書生」:百無一用(的東西)⊇ 書生;這其實是倒裝寫法,我懷疑「佛教是文學,哲學,科學」本應寫為「文學,哲學,科學皆是佛學」。
「強人是你,能頂天立地」:強人∋ 你;這也是倒裝法。
當然啦,「是」還有其他用法。
「是其是」:第一個「是」意思為「贊成,支持」,第二個「是」意思為「正確的事」;全句為「贊成正確的事」。
當然啦,此乃我極膚淺的分析。很多時候,文學作者故意利用模棱兩可的觀念創作,這也算留白罷!
或者正如我朋友所說,不要時常太執着於正確的意思:世上多數東西都只有「相對正確」,沒有「絕對正確」。
意大利粉神教

原教旨基督教的最大對手是誰?
原教旨回教徒?不是,他們沒有像美國般的超級大國撐腰!
其他的基督教派?這不算對手罷,頂多只是教義詮釋不同而已!
告訴你吧,是意大利粉神教(Church of the Flying Spaghetti Monsterism)。噢,未聽過?它的每個教義都衝着神創論(Creationism,新稱智慧設計論 Intelligent Design)而來。
據說每個支持智慧設計論的證據,都可以支持意大利粉神教。
該教派已向美國各州政府發公開信:美國學校的生物科若要教授智慧設計論,作為進化論的代替理論,則應同時教授意大利粉神教。
若閣下已開始厭倦『訓教』,是時候考慮意大利粉神教,總比信飛碟教(真道教)好,起碼不用作出金錢奉獻!(哈哈!)
註:若此篇文章令基督徒感覺冒犯,請多多吃意大利粉及多多包涵!
Sunday, April 02, 2006
科學與宗教
語文是非常奇怪的東西,同一句說話,可以有極端不同的意思。
在上一篇我認為可以說「科學是佛教」,不可以說「佛教是科學」;我的朋友旋即撰文反對,但似乎只是誤解。
他認為科學是佛教的一部分,並非全部,所以不好說「科學是佛教」;但「白馬是馬」,「西施狗是狗」,「量子力學是物理」,其中的「是」都意味着「部分」。
他認為「佛教是科學」並無不妥,而且佛教同時是文學及哲學;但他心中的「是」意義是「包容」,不過我也聽過一些信徒說「因為佛教是科學,所以可信」。
心境不同,層次不同,使得一句說話有不同的意思。
宗教與科學的關係,千絲萬縷:化學源於煉金術,天文始於星相學,宗教可促進科學;教廷曾封殺日心說,全屍觀念不容解剖學,宗教亦可扯科學後腿。找出平衡絕非易事!
若一些科學理論與宗教觀念不相容,提倡者經常被斥為異端。例如:進化論者常被原教旨基督教徒視為無神論者,雖然有不少進化論者是基督徒(參看www.talkorigins.org)。
真正視科學為絕對的應是唯物論者,他們認為心靈也是由物質所決定。當然唯物論也可算是一種信仰。
不要混淆科學教派(scientology),它的教義雖說相信科學,但它所相信的“科學”被多數學者歸類為偽科學!
在上一篇我認為可以說「科學是佛教」,不可以說「佛教是科學」;我的朋友旋即撰文反對,但似乎只是誤解。
他認為科學是佛教的一部分,並非全部,所以不好說「科學是佛教」;但「白馬是馬」,「西施狗是狗」,「量子力學是物理」,其中的「是」都意味着「部分」。
他認為「佛教是科學」並無不妥,而且佛教同時是文學及哲學;但他心中的「是」意義是「包容」,不過我也聽過一些信徒說「因為佛教是科學,所以可信」。
心境不同,層次不同,使得一句說話有不同的意思。
宗教與科學的關係,千絲萬縷:化學源於煉金術,天文始於星相學,宗教可促進科學;教廷曾封殺日心說,全屍觀念不容解剖學,宗教亦可扯科學後腿。找出平衡絕非易事!
若一些科學理論與宗教觀念不相容,提倡者經常被斥為異端。例如:進化論者常被原教旨基督教徒視為無神論者,雖然有不少進化論者是基督徒(參看www.talkorigins.org)。
真正視科學為絕對的應是唯物論者,他們認為心靈也是由物質所決定。當然唯物論也可算是一種信仰。
不要混淆科學教派(scientology),它的教義雖說相信科學,但它所相信的“科學”被多數學者歸類為偽科學!
Subscribe to:
Comments (Atom)